[Recent Entries][Archive][Friends][User Info]
| Time | Text |
|---|---|
| 06:45 pm [Link] |
Теория письма Сразу скажу, что излагаемое мною ниже кажется мне настолько простым, что я уверен, что нечто подобное уже было придумано кем-нибудь раньше. Было бы замечательно, если кто-то сможет дать ссылку. В начале сентября я задумался над тем, почему мы пишем так, а не иначе. Я имею ввиду наш алфавит и способ его написания. Например, русская буква «А» взята из греческого, в котором она называлась «альфа». Финикийцы, у которых греки позаимствовали эту букву, рисовали её повёрнутой на прямой угол против часовой стрелки относительно её нынешнего положения и называли её алеф, что переводится как бык. Само написание буквы напоминало голову быка. Точно такая же ситуация имеет место для многих других букв — например, буква «Д» в финикийском называлась далет, что переводится как палатка, а написание буквы напоминало треугольный вход в палатку. Этим начертания существуют более трёх тысяч лет, и на их основе были созаданы алфавиты греческого и арабского языков, иврита, а также другие алфавиты на их основе, использовавшиеся в столь отдалённых областях, как Монголия. Финикийский язык уже мёртв полторы тысячи лет, а буквы его остались с нами по историческим причинам. (Я не специалист по древним письменностям, поэтому в вышеприведённом очерке наверняка есть ошибки.) Мне стало интересно, а каким мог бы быть алфавит, если бы нам пришлось создавать его с нуля, не опираясь на ранее созданные алфавиты. Я решил исходить из того, что алфавит должен быть удобным при рукописном написании. Будем считать, что мы рисуем линии на ровной твёрдой поверхности пером нулевой толщины, не отрывая его от бумаги. Какие вообще линии мы можем нарисовать? Видимо, следует принять, что положение пера должно быть непрерывно дифференцируемой функцией из [0, 1] в плоскость, что следует хотя бы из существования ускорения. Что ещё? Ясно, что человек — не робот, и не может провести линию точно через заданную точку. Поэтому мы должны исключить тройные самопересечения, равно как и совпадение начальной или конечной точки с какой-то другой точкой. Далее, человек не робот и не в состоянии держать свою руку неподвижно — наши мышцы всегда дрожат, хотя бы чуть-чуть. Поэтому скорость пера всегда должна быть отлична от нуля. (Если кто-то несогласен с этим предположением, то он может прочесть ниже возможный вариант разрешения этой трудности.) Суммируя сказанное, можно сказать, что человек умеет рисовать только иммерсии общего положения отрезка в плоскость. Такие отображения мы будем называть линиями. Заметим, что если к линии прибавить достаточно малую (в равномерной норме по функции и её производной) непрерывно дифференцируемую функцию, то мы снова получим линию. Вряд ли мы хотим считать различными линии, которые можно получить друг из друга непрерывной деформацией. Поэтому назовём две линии эквивалентными, если одну из них можно перевести в другую непрерывно дифференцируемой гомотопией в классе линий. (Здесь, кстати, надо отметить, что линии ориентированные, и это правильно, как мы увидим ниже.) Я утверждаю, что человек в состоянии нарисовать представителя любого класса эквивалентности по указанному выше отношению. Действительно, для этого не надо совершать никаких «тонких» действий, а надо лишь «грубо» начертить линию. В дальнейшем я не различаю линию и её класс эквивалентности. Как это применить к письменности? Мы хотим писать слова, не отрывая перо от бумаги. Слова состоят из букв. Мы должны иметь возможность составить слово из произвольной последовательности букв, приписывая их рядом. Определим операцию соединения линий также, как композицию классов петель в фундаментальной группе: новое отображение отрезка в плоскость будет совпадать с первым отображением на своей первой половине и со вторым — на второй половине. При этом надо выбрать представителей классов эквивалентности так, чтобы результирующее отображение было линией, и при этом не возникло бы новых точек пересечения. При этих условиях операция соединения определяется однозначно. Легко видеть, что мы получили некоммутативный моноид. Роль нейтрального элемента играет вложение отрезка в плоскость. Это вложение мы будем называть тривиальной линией. Заметим, что если мы хотим соединять буквы привычным нам образом, то начало и конец линии буквы должны находиться в некомпактной компоненте связности — иначе нам придётся вписывать одну букву внутрь другой. Будем называть такие линии внешними. Не важдый набор внешних линий можно использовать в качестве алфавита. Необходимо избежать неоднозначности при разборе линий на составные части. Заметим, что любая внешняя линия однозначно представляется в виде соединения нетривиальных линий, каждую из которых нельзя разложить в соединения двух нетривильных линий. Такие линии будем называть простыми. Простых линий счётное число. Теперь легко понять, что моноид линий — это свободный моноид с однозначно определённым набором образующих, которыми являются простые линии. Поэтому естественно в качестве алфавита взять простые линии. Мы получаем неограниченный запас букв на все случаи жизни. Буквы естественным образом классифицируются по количеству точек самопересечения. Заметим, что зеркальная симметрия буквы даёт другую букву с тем же число точек самопересечения. На рисунке представлены буквы с 1, 2 и 3 точками самопересечения, при этом зеркально-симметричные буквы опущены. Левая концевая точка начальная, правая — конечная. Отметим, что в списке есть буквы, отличающиеся только ориентацией. 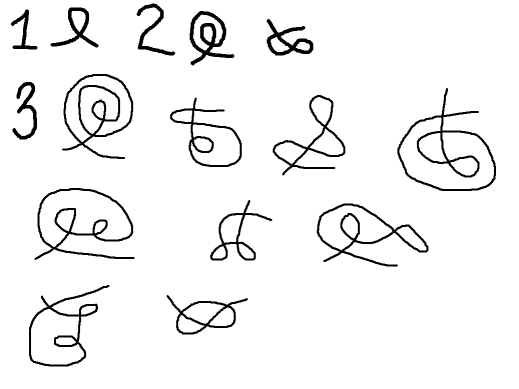 Ясно, что теорию можно обобщать, допуская, например изломы. На этом пути, по-видимому, можно получить решение указанной выше проблемы нулевой скорости. Немаловажное практическое замечание: как легко видеть на рисунке, наиболее частым элементом является простая петля. На практике такие петли можно было бы заменить изломами (с разными касательными прямыми слева и справа и требованием оставаться в этом классе при гомотопии). Если кому-нибудь это интересно, можно попробовать составить алфавит для русского языка и записать на нём что-нибудь. |
| Reply: | |