blackpost: Квантовый компьютер.

Квантовый компьютер.

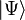Один кубит можно представить в виде электрона в двух ямном потенциале, так что $|0\rangle$ означает нахождение его в левой яме, а $|1\rangle$ — в правой. Это называется кубит на зарядовых состояниях. Общий вид квантового состояния такого электрона: $|\Psi\rangle=\lambda_0|0\rangle+\lambda_1|1\rangle$ . Зависимость его от времени есть зависимость от времени амплитуд $\lambda_0,\ \lambda_1$ ; она задается уравнением Шредингера вида $ih\frac{\partial\Psi}{\partial t}\Psi=H\Psi$ где гамильтониан $H$ имеет в силу одинакового вида ям и эрмитовости вид $\left(\begin{array}{lll}&a\ &-a\\<br />&-a\ &a\end{array}\right)$ для некоторой константы $a$ , так что вектор $|\tilde 0\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle )$ есть собственный вектор этого гамильтониана с собственным значением 0 (так называемое основное состояние), а $|\tilde 1\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle )$ — собственный вектор со значением $2a$ (первое возбужденное состояние). Никаких других собственных состояний (с определенным значением энергии) здесь нет, так как наша задача двумерная. Поскольку каждое состояние $|\Psi\rangle$ переходит за время $t$ в состояние $\lambda_0exp(0t)|\tilde 0\rangle+\lambda_1exp(-2at/h)|\tilde 1\rangle$ , то для реализации операции NOT (перехода $|0\rangle ->|1\rangle$ и наоборот достаточно просто подождать время $t=\pi h/2a$ . То есть гейт NOT дается просто естественной квантовой эволюцией нашего кубита при условии, что внешний потенциал задает двух ямную структуру; это делается с помощью технологии квантовых точек.

Для реализации CNOT надо расположить два кубита (то есть две пары ям) перпендикулярно друг другу, и в каждой из них расположить по отдельному электрону. Тогда константа $a$ для первой (управляемой) пары ям будет зависеть от того, в каком состоянии находится электрон во второй (управляющей) паре ям: если ближе к первой, $a$ будет больше, если дальше — меньше. Поэтому состояние электрона во второй паре определяет время совершения NOT в первой яме, что позволяет снова выбрать нужную длительность времени для производства операции CNOT.

Эта схема очень приблизительная и идеализирована; реальные схемы сложнее и их реализация представляет вызов экспериментальной физике