[Most Recent Entries] [Calendar View]
Monday, January 11th, 2016
| Time | Event |
| 6:35a | Использование МатАнализа в компьютерных играх (часть 2) Ключевые слова: Задача о коллекции; Wolfram Alpha; Wolfram Mathematica; числа Стирлинга второго рода; матанализ; теория вероятностей; мат ожидание; медиана; квантиль; компьютерные игры; коллекция вкладышей; функция распределения случайной величины; плотность вероятности, ArcheAge. ВведениеКогда остается заполучить только три из ста предметов для того чтобы собрать всю коллекцию (вкладышей жвачек БомБимБома или Турбо, или набора тяжелых доспехов для персонажа компьютерной игры), то огонь в глазах и ожидание чуда вытесняют и логику и разум и попытки математического анализа из головы напрочь. Есть только одна мысль «Ещё чуть-чуть и я заполучу оставшееся! Я соберу всю!». В это время, родные и друзья, этого одержимого коллекционера озадачены лишь только одним вопросом – «А, чуть-чуть, это сколько?!». Сколько маме нужно купить ещё ненавистных жвачек, или сколько нужно ещё девушке сидеть одной, пока её парень не выбьет с монстров в игре «редчайшие трусы Баала»?! Ответить на вопрос «сколько нужно купить жевательных резинок, чтобы собрать полную коллекцию из N-штук вкладышей» сходу довольно сложно, даже если пользоваться Яндексом, потому, что сложно сформулировать сам запрос для «обычного» поисковика. Попытка решения задачи самостоятельно обычно ставит людей в тупик – не понятно, с какой стороны к ней подступиться. В данной статье будут рассмотрены три вопроса: Как подходить к задачам, которые не понятно на первый взгляд как решать? Каким поисковиком пользоваться для того чтобы получать научные ответы на научные вопросы (а не получать предложения купить формулу квадратного уравнения на eBay)? И конечно, сколько же нужно купить жвачек, чтобы собрать коллекцию вкладышей? Читать дальше → |
| 11:05a | [Перевод] Новое в Wolfram Language | Аналитическое решение уравнений в частных производных  Перевод поста Devendra Kapadia "New in the Wolfram Language: Symbolic PDEs". Код, приведенный в статье, можно скачать здесь. Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации. Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3. История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами. Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t: 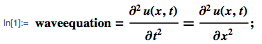 Читать дальше → |
| 8:38p | Вычисление биномиальных коэффициентов… вручную Ранее в двух статьях была затронута тема вычисления биномиальных коэффициентов с помощью компьютера. Расчет биномиальных коэффициентов на Си (С++) Расчет биномиальных коэффициентов с использованием Фурье-преобразований По их прочтению может сложиться мнение что это сложная и ресурсоемкая задача. Прежде чем программировать что-то, попробуем разобраться что здесь к чему. Факториальная формула: 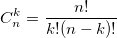 Раскроем ее: 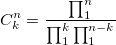 Очевидно, что 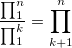 и тогда и тогда 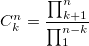 А теперь попробуем посчитать например 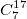 : :Читать дальше → |
| << Previous Day |
2016/01/11 [Calendar] |
Next Day >> |