|
|
| Пишет schegloff ( @ 2008-10-04 10:52:00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Холопский путь в СТО - 2А, или Два графика, с которого он начался
Обещал - делаю. Некоторое время назад, основываясь на аналитической модели![[info]](http://lj.rossia.org/img/userinfo-lj.gif) kaktus77@lj, я составил табличку в Экселе для расчета полета на Альфу Центавра с постоянным ускорением в 1g. Вместо вывода аналитических формул я применил численное интегрирование исходных дифференциальных уравнений, убедился, что интегрирование сходится к формульным значениям, и позволил себе немножко поиграться параметрами модели.
kaktus77@lj, я составил табличку в Экселе для расчета полета на Альфу Центавра с постоянным ускорением в 1g. Вместо вывода аналитических формул я применил численное интегрирование исходных дифференциальных уравнений, убедился, что интегрирование сходится к формульным значениям, и позволил себе немножко поиграться параметрами модели.
Итак, в случае, когда мы ускоряемся до половины пути (по часам звездолета) к Альфе, разворачиваем тягу двигателей в обратную сторону, тормозим около Альфы до нуля, снова разгоняемся обратно к Земле, на половине обратного пути опять разворачиваем тягу и тормозим до нуля аккурат в окрестностях Земли, - для земного времени с точки зрения звездолета получается следующий график:
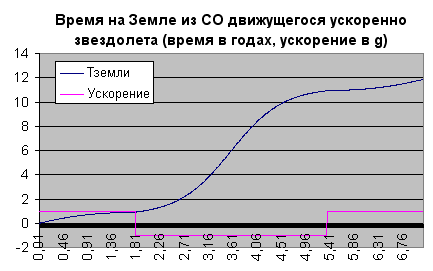
Парадокс близнецов перестал быть парадоксом: в какой СО ни считай, а на Земле все равно проходит больше времени, чем на звездолете.
Однако если на этом не тормозить, и вместо возвращения к Земле продолжить лететь в сторону Альфы, вторично развернув тягу чуть раньше - то получится куда более интересный график:
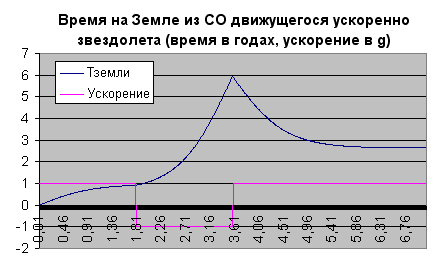
Как видите, время на Земле, рассчитанное в СО звездолета, благополучно пошло в обратную сторону. Лично мне такой результат представляется еще худшей проблемой, чем исходный "парадокс близнецов". Вот почему я и взялся за "холопский путь".
Холопский путь в СТО - 1
Холопский путь в СТО - 2
P.S. Буду благодарен френдам за выведение этой записи в топ. Может быть, на огонек заглянут настоящие спецы по СТО, и подскажут, как разрешить все эти парадоксы.
Обещал - делаю. Некоторое время назад, основываясь на аналитической модели
![[info]](http://lj.rossia.org/img/userinfo-lj.gif) kaktus77@lj, я составил табличку в Экселе для расчета полета на Альфу Центавра с постоянным ускорением в 1g. Вместо вывода аналитических формул я применил численное интегрирование исходных дифференциальных уравнений, убедился, что интегрирование сходится к формульным значениям, и позволил себе немножко поиграться параметрами модели.
kaktus77@lj, я составил табличку в Экселе для расчета полета на Альфу Центавра с постоянным ускорением в 1g. Вместо вывода аналитических формул я применил численное интегрирование исходных дифференциальных уравнений, убедился, что интегрирование сходится к формульным значениям, и позволил себе немножко поиграться параметрами модели.Итак, в случае, когда мы ускоряемся до половины пути (по часам звездолета) к Альфе, разворачиваем тягу двигателей в обратную сторону, тормозим около Альфы до нуля, снова разгоняемся обратно к Земле, на половине обратного пути опять разворачиваем тягу и тормозим до нуля аккурат в окрестностях Земли, - для земного времени с точки зрения звездолета получается следующий график:

Парадокс близнецов перестал быть парадоксом: в какой СО ни считай, а на Земле все равно проходит больше времени, чем на звездолете.
Однако если на этом не тормозить, и вместо возвращения к Земле продолжить лететь в сторону Альфы, вторично развернув тягу чуть раньше - то получится куда более интересный график:

Как видите, время на Земле, рассчитанное в СО звездолета, благополучно пошло в обратную сторону. Лично мне такой результат представляется еще худшей проблемой, чем исходный "парадокс близнецов". Вот почему я и взялся за "холопский путь".
Холопский путь в СТО - 1
Холопский путь в СТО - 2
P.S. Буду благодарен френдам за выведение этой записи в топ. Может быть, на огонек заглянут настоящие спецы по СТО, и подскажут, как разрешить все эти парадоксы.