|
|
| Пишет schegloff ( @ 2008-09-30 23:03:00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Холопский путь в СТО - 2, или Парадокс часов
Кто не читал первую часть, рекомендую сначала ознакомиться. Ну а кто уже читал, может смело лезть под кат.
Через несколько дней капитан снова вызывает теоретика к себе. Ты был прав, говорит он, прикуривая новую сигару от предыдущей. Мы получили ответный сигнал, и время на втором звездолете оказалось то самое, 1.732. Хуже того, мы получили от них еще и аналогичный нашему запрос. Думаю, не надо говорить, в какой момент. Для нас время замедлено у них, для них - у нас. Но так не бывает. Я скорее поверю в то, что свет летит от нас к ним и обратно с разной скоростью, чем в то, что на чужом звездолете замедляется время только потому, что мы обмениваемся с ним сигналами. Нужно проверить твои предсказания чем-то посущественнее, чем свет. Так вот, к нам приближается еще один звездолет, и я уже столковался с его капитаном...
Задача третья. Звездолет 1 и звездолет 2 синхронизировали часы в момент 0 и разлетелись в разные стороны с относительной скоростью 0.5с. Через некоторое время к звездолету 1 приблизился звездолет 3, летящий вслед за звездолетом 2 со скоростью (относительно звездолета 1) 0.8с. В момент t = 2 ед. времени по часам звездолета 1 часы звездолетов 1 и 3 также были синхронизированы. Когда звездолет 3 догонит звездолет 2, он снова произведет синхронизацию часов (замер собственного времени и времени звездолета 2 в момент встречи), и сообщит об этом на звездолет 1. Требуется рассчитать промежутки времени между синхронизациями, прошедшие по часам звездолетов 2 и 3.
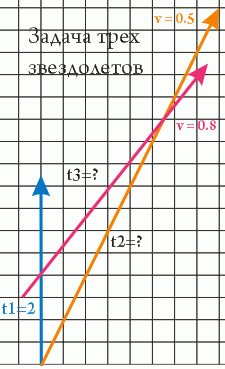
Теоретик довольно потирает руки и приступает к решению задачи. Прежде всего, в нашей теории относительности остался один невыясненный момент. Мы знаем скорости звездолетов 2 и 3 относительно нас; а вот какой будет их скорость относительно друг друга? На первый взгляд, 0.3 = 0.8 - 0.5? Но это только на первый взгляд - времена и расстояния у них другие, поэтому и относительная скорость может быть другой. Воспользуемся методом коэффициента k и выведем формулу для расчета относительных скоростей:
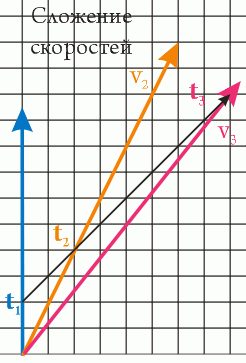
Как найти скорость v3, зная относительные скорости v12 = v2 и v23 (3-го звездолета относительно второго)? Как видно из схемы, t2 = k12*t1, и точно так же t3 = k23*t2. Таким образом, k13*t = k12*k23*t1, откуда
k(v1+v2) = k(v1) * k(v2)
Поскольку (см. часть 1) v = (k2-1)/(k2+1), можно подставить на место k для суммарной скорости выражения для k1 и k2 ( формулу (1) из первой части, k = SQRT((1+v)/(1-v)) ), произвести необходимые упрощения и получить в результате:
v = (v1+v2)/(1+v1*v2)
Для нашего случая v23 = (0,8-0,5) / (1 - 0,8*0,5) = 0,5. Теперь мы можем решить задачу в 2-х вариантах - для неподвижного (исходная) и для движущегося звездолета:
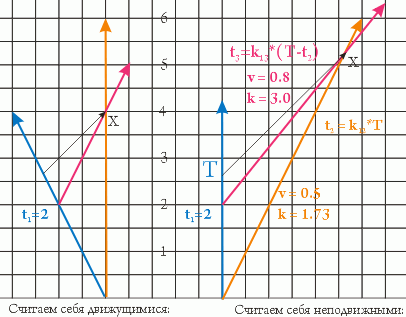
Если считать нас (звездолет 1) движущимися, все просто: t1 = 2, t3 = 2 из соображений симметрии (скорости одинаковы), t2 = 4 по часам движущегося звездолета, которые замедлены на величину SQRT(1-0.5^2) - а значит, по собственным часам t2 = 4/SQRT(1-0.5^2) = 4.62 ед.
Если считать звездолет 1 неподвижным, то нужно определить координаты встречи звездолетов 2 и 3. К моменту встречи они пролетят от начала координат равные расстояния, т.е. v2*tx = v3*(tx-t1), откуда tx = v3*t1 / (v3-v2) = 0.8*2/(0.8-0.5) = 5.33 ед, а расстояние x = v2*tx = 0.5*5.33 = 2.66 ед. Чтобы сигнал, отправленный с первого звездолета в T, достиг остальных звездолетов как раз в момент встречи, T = tx - x*c = 5.33 - 2.66*1 = 2.66 ед. Теперь у нас есть все данные, чтобы посчитать t2 и t3 через коэффициент k:
t2 = T*k2 = 2.66*1.73 = 4.62
t3 = (T-t1)*k3 = 0.66*3 = 2
Как видите, все сходится. Суммарное время звездолетов 1 и 3, затраченное на попадание в точку X, окажется меньше, чем время, которое затратит на это звездолет 2. Так что, мой капитан, время на быстролетящих звездолетах замедляется на самом деле.
В ответ капитан качает головой. Разумеется, расчетное время замедляется, говорит он. По вашей же формуле, время на третьем звездолете идет медленнее, чем на нашем, у нас 1 секунда, у них SQRT(1-0.8^2) - только 0.6 секунд. Поэтому ничего удивительного, что при синхронизизации с нами в 2 ед = 0, его часы в наши 5.33 = 2 + 3.33 покажут 2 = 0 +3.33*0.6 единицы. Но точно так же и на звездолете 3 могут посчитать, что время на нашем звездолете идет медленнее, чем у них, в той же пропорции, и что в момент, когда у нас был 0 ед, у них часы показывали -3.33 = -2/0,6. Таким образом, с нашей (звездолета 1) точки зрения, встреча звездолетов 2 и 3 произошла в 5.33 ед., с точки зрения звездолета 3 - тоже в 5.33 ед (2 + 3.33), а вот с точки зрения звездолета 2 - в 4.62 ед. Ну а теперь скажите, так у кого же на самом деле замедляется время? У суммы двух разных времен, посчитанных на разных звездолетах?
Да, у суммы времен, отвечает теоретик. Задача была на определение показания часов при трех последовательных синхронизациях. Она решена, с результатом вы согласились. При последовательности синхронизаций вида 1-2, 1-3, 3-2 сумма времен (1-3) и (3-2) будет меньше, чем время, прошедшее на звездолете 2. Если это - не замедление времени, то что же это?!
Капитан мрачно расчесывает бороду. Замедление времени, говорит он, это когда время замедляется по каким-то одним часам. Иначе можно измерить наш звездолет тремя рулетками по схеме "1-2, 1-3 и 3-2", получить, что (1-3) и (3-2) вместе длиннее, чем (1-2) и сделать отсюда вывод, что у нас появились лишние каюты. Как только мы начинаем измерять все времена по одним часам, всякое абсолютное замедление исчезает. По часам звездолетов 1 и 3, летящих со скоростью 0.5 относительно звездолета 2, между событиями проходит 5.33 единиц, по часам звездолета 2 - 4.66 единиц. Если мимо звездолета 2 пролетит в нашем направлении какой-нибудь звездолет 3' - то ситуация будет в точности симметрична:
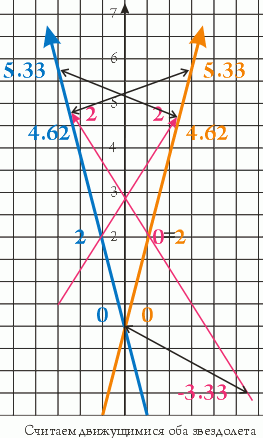
Поскольку 5.33 > 4.62, то время окажется медленнее на звездолете 2, который в обеих случаях считался движущимся. А вот если мы посмотрим на те же события с его точки зрения (звездолета 2), продолжает вошедший в раж капитан, то все будет наоборот. На самом звездолете 2 пройдет 4.66 единиц. Однако время на звездолетах 1 и 3 течет медленнее, с коэффициентом SQRT(1-0,5^2)=0.866, поэтому у них, с точки зрения звездолета 2 (и это подтвердит радиолокация!) пройдет только по 4 единицы. Снова время идет медленнее на тех звездолетах, который мы считаем движущимися!
Так вот, уважаемый теоретик, я никак не возьму в голову, что же это за время такое в вашей теории. Отсюда оно медленее, а отсюда - уже быстрее. Может быть, в теории что-то подправить?
Как видите, худшие опасения сбылись. Капитан звездолета не только додумался до парадокса часов, но еще и сформулировал в виде конкретной претензии к новосозданной теории относительности. Распространяется ли принцип относительности на скорость времени разных звездолетов? Носит ли "замедление" времени чисто условный, расчетный характер - или же может быть как-то обнаружено в рамках нашего модельного мира (движущиеся с постоянной скоростью звездолеты в двумерном пространстве-времени)? Как правильно считать суммарное время двух релятивистских звездолетов - простым суммированием показаний часов, или пересчитывать их на время звездолета, для которого в конечном счете производится расчет?
Как вы наверняка уже догадались, ответы на эти вопросы я так и не смог найти. Холопский путь в СТО закончился, не успев толком начаться. Итогом его оказался эпиграф, которым я и хочу закончить свое нерадостное повествование:
Что же такое время? Если никто меня об этом не спрашивает, я знаю, что такое время; если бы я захотел объяснить спрашивающему – нет, не знаю. Аврелий Августин, 398 год н.э.
Кто не читал первую часть, рекомендую сначала ознакомиться. Ну а кто уже читал, может смело лезть под кат.
Через несколько дней капитан снова вызывает теоретика к себе. Ты был прав, говорит он, прикуривая новую сигару от предыдущей. Мы получили ответный сигнал, и время на втором звездолете оказалось то самое, 1.732. Хуже того, мы получили от них еще и аналогичный нашему запрос. Думаю, не надо говорить, в какой момент. Для нас время замедлено у них, для них - у нас. Но так не бывает. Я скорее поверю в то, что свет летит от нас к ним и обратно с разной скоростью, чем в то, что на чужом звездолете замедляется время только потому, что мы обмениваемся с ним сигналами. Нужно проверить твои предсказания чем-то посущественнее, чем свет. Так вот, к нам приближается еще один звездолет, и я уже столковался с его капитаном...
Задача третья. Звездолет 1 и звездолет 2 синхронизировали часы в момент 0 и разлетелись в разные стороны с относительной скоростью 0.5с. Через некоторое время к звездолету 1 приблизился звездолет 3, летящий вслед за звездолетом 2 со скоростью (относительно звездолета 1) 0.8с. В момент t = 2 ед. времени по часам звездолета 1 часы звездолетов 1 и 3 также были синхронизированы. Когда звездолет 3 догонит звездолет 2, он снова произведет синхронизацию часов (замер собственного времени и времени звездолета 2 в момент встречи), и сообщит об этом на звездолет 1. Требуется рассчитать промежутки времени между синхронизациями, прошедшие по часам звездолетов 2 и 3.

Теоретик довольно потирает руки и приступает к решению задачи. Прежде всего, в нашей теории относительности остался один невыясненный момент. Мы знаем скорости звездолетов 2 и 3 относительно нас; а вот какой будет их скорость относительно друг друга? На первый взгляд, 0.3 = 0.8 - 0.5? Но это только на первый взгляд - времена и расстояния у них другие, поэтому и относительная скорость может быть другой. Воспользуемся методом коэффициента k и выведем формулу для расчета относительных скоростей:

Как найти скорость v3, зная относительные скорости v12 = v2 и v23 (3-го звездолета относительно второго)? Как видно из схемы, t2 = k12*t1, и точно так же t3 = k23*t2. Таким образом, k13*t = k12*k23*t1, откуда
k(v1+v2) = k(v1) * k(v2)
Поскольку (см. часть 1) v = (k2-1)/(k2+1), можно подставить на место k для суммарной скорости выражения для k1 и k2 ( формулу (1) из первой части, k = SQRT((1+v)/(1-v)) ), произвести необходимые упрощения и получить в результате:
v = (v1+v2)/(1+v1*v2)
Для нашего случая v23 = (0,8-0,5) / (1 - 0,8*0,5) = 0,5. Теперь мы можем решить задачу в 2-х вариантах - для неподвижного (исходная) и для движущегося звездолета:

Если считать нас (звездолет 1) движущимися, все просто: t1 = 2, t3 = 2 из соображений симметрии (скорости одинаковы), t2 = 4 по часам движущегося звездолета, которые замедлены на величину SQRT(1-0.5^2) - а значит, по собственным часам t2 = 4/SQRT(1-0.5^2) = 4.62 ед.
Если считать звездолет 1 неподвижным, то нужно определить координаты встречи звездолетов 2 и 3. К моменту встречи они пролетят от начала координат равные расстояния, т.е. v2*tx = v3*(tx-t1), откуда tx = v3*t1 / (v3-v2) = 0.8*2/(0.8-0.5) = 5.33 ед, а расстояние x = v2*tx = 0.5*5.33 = 2.66 ед. Чтобы сигнал, отправленный с первого звездолета в T, достиг остальных звездолетов как раз в момент встречи, T = tx - x*c = 5.33 - 2.66*1 = 2.66 ед. Теперь у нас есть все данные, чтобы посчитать t2 и t3 через коэффициент k:
t2 = T*k2 = 2.66*1.73 = 4.62
t3 = (T-t1)*k3 = 0.66*3 = 2
Как видите, все сходится. Суммарное время звездолетов 1 и 3, затраченное на попадание в точку X, окажется меньше, чем время, которое затратит на это звездолет 2. Так что, мой капитан, время на быстролетящих звездолетах замедляется на самом деле.
В ответ капитан качает головой. Разумеется, расчетное время замедляется, говорит он. По вашей же формуле, время на третьем звездолете идет медленнее, чем на нашем, у нас 1 секунда, у них SQRT(1-0.8^2) - только 0.6 секунд. Поэтому ничего удивительного, что при синхронизизации с нами в 2 ед = 0, его часы в наши 5.33 = 2 + 3.33 покажут 2 = 0 +3.33*0.6 единицы. Но точно так же и на звездолете 3 могут посчитать, что время на нашем звездолете идет медленнее, чем у них, в той же пропорции, и что в момент, когда у нас был 0 ед, у них часы показывали -3.33 = -2/0,6. Таким образом, с нашей (звездолета 1) точки зрения, встреча звездолетов 2 и 3 произошла в 5.33 ед., с точки зрения звездолета 3 - тоже в 5.33 ед (2 + 3.33), а вот с точки зрения звездолета 2 - в 4.62 ед. Ну а теперь скажите, так у кого же на самом деле замедляется время? У суммы двух разных времен, посчитанных на разных звездолетах?
Да, у суммы времен, отвечает теоретик. Задача была на определение показания часов при трех последовательных синхронизациях. Она решена, с результатом вы согласились. При последовательности синхронизаций вида 1-2, 1-3, 3-2 сумма времен (1-3) и (3-2) будет меньше, чем время, прошедшее на звездолете 2. Если это - не замедление времени, то что же это?!
Капитан мрачно расчесывает бороду. Замедление времени, говорит он, это когда время замедляется по каким-то одним часам. Иначе можно измерить наш звездолет тремя рулетками по схеме "1-2, 1-3 и 3-2", получить, что (1-3) и (3-2) вместе длиннее, чем (1-2) и сделать отсюда вывод, что у нас появились лишние каюты. Как только мы начинаем измерять все времена по одним часам, всякое абсолютное замедление исчезает. По часам звездолетов 1 и 3, летящих со скоростью 0.5 относительно звездолета 2, между событиями проходит 5.33 единиц, по часам звездолета 2 - 4.66 единиц. Если мимо звездолета 2 пролетит в нашем направлении какой-нибудь звездолет 3' - то ситуация будет в точности симметрична:

Поскольку 5.33 > 4.62, то время окажется медленнее на звездолете 2, который в обеих случаях считался движущимся. А вот если мы посмотрим на те же события с его точки зрения (звездолета 2), продолжает вошедший в раж капитан, то все будет наоборот. На самом звездолете 2 пройдет 4.66 единиц. Однако время на звездолетах 1 и 3 течет медленнее, с коэффициентом SQRT(1-0,5^2)=0.866, поэтому у них, с точки зрения звездолета 2 (и это подтвердит радиолокация!) пройдет только по 4 единицы. Снова время идет медленнее на тех звездолетах, который мы считаем движущимися!
Так вот, уважаемый теоретик, я никак не возьму в голову, что же это за время такое в вашей теории. Отсюда оно медленее, а отсюда - уже быстрее. Может быть, в теории что-то подправить?
Как видите, худшие опасения сбылись. Капитан звездолета не только додумался до парадокса часов, но еще и сформулировал в виде конкретной претензии к новосозданной теории относительности. Распространяется ли принцип относительности на скорость времени разных звездолетов? Носит ли "замедление" времени чисто условный, расчетный характер - или же может быть как-то обнаружено в рамках нашего модельного мира (движущиеся с постоянной скоростью звездолеты в двумерном пространстве-времени)? Как правильно считать суммарное время двух релятивистских звездолетов - простым суммированием показаний часов, или пересчитывать их на время звездолета, для которого в конечном счете производится расчет?
Как вы наверняка уже догадались, ответы на эти вопросы я так и не смог найти. Холопский путь в СТО закончился, не успев толком начаться. Итогом его оказался эпиграф, которым я и хочу закончить свое нерадостное повествование:
Что же такое время? Если никто меня об этом не спрашивает, я знаю, что такое время; если бы я захотел объяснить спрашивающему – нет, не знаю. Аврелий Августин, 398 год н.э.