|
|
| Пишет ivanov_petrov ( @ 2008-12-07 12:19:00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фракталы

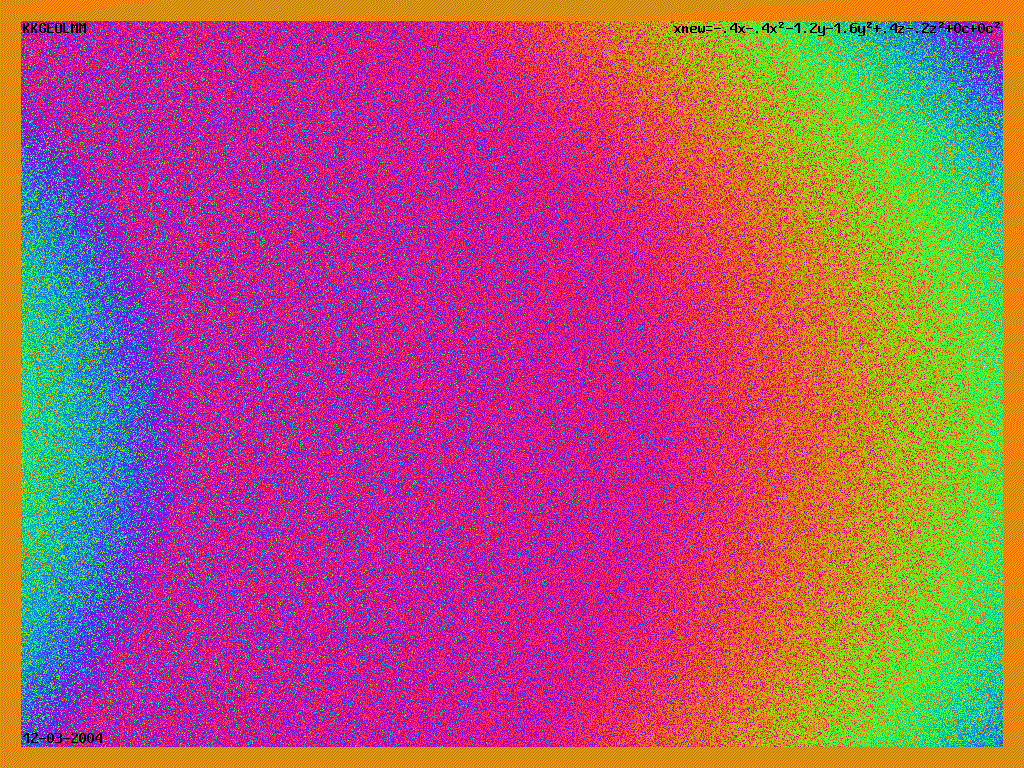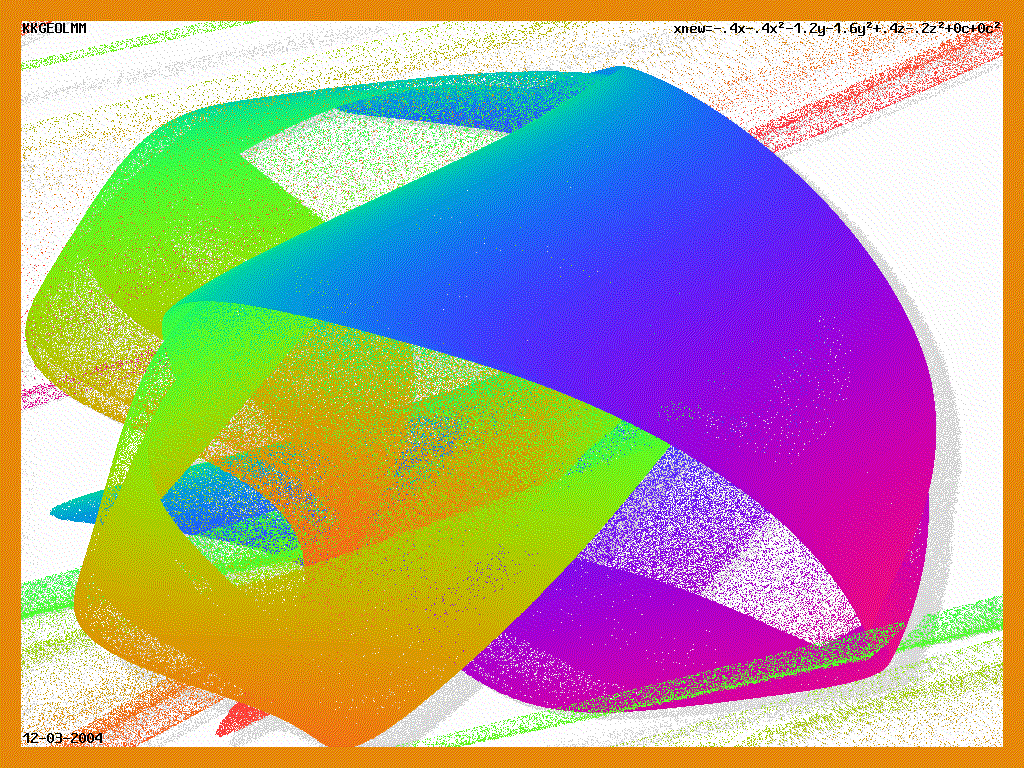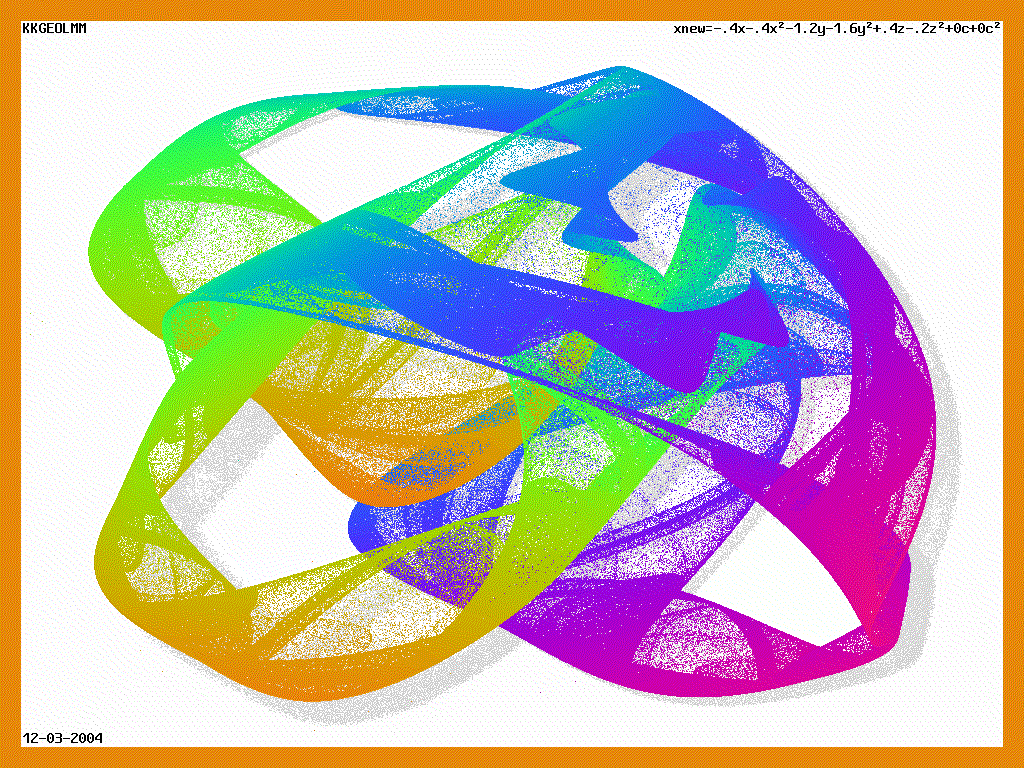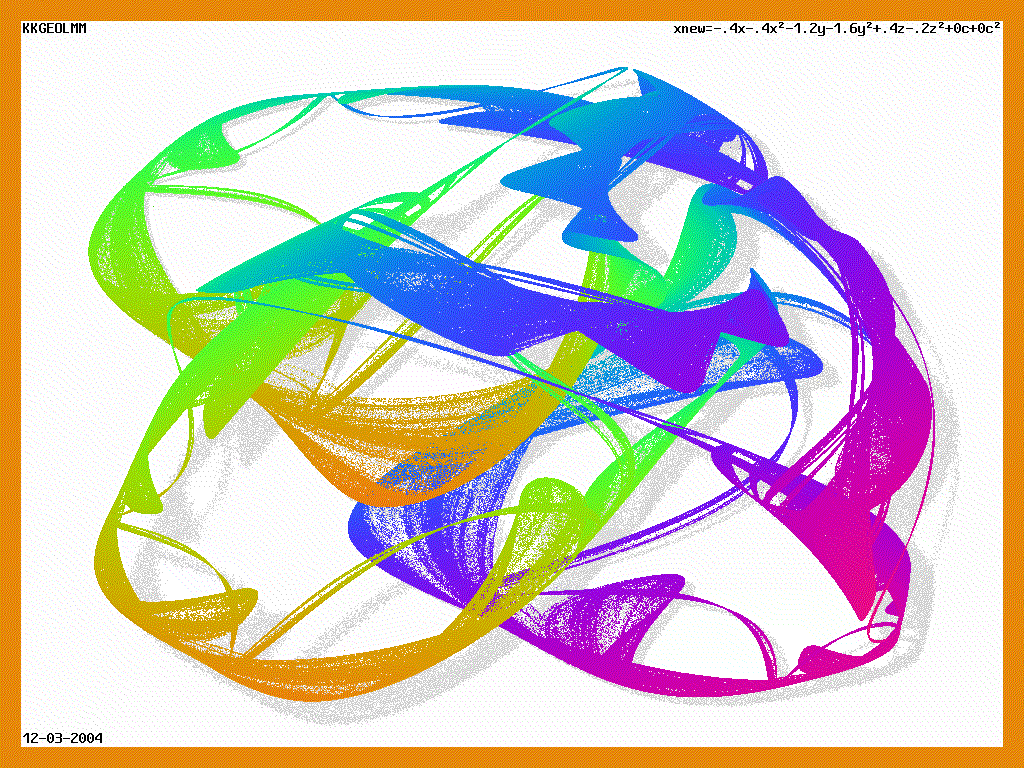
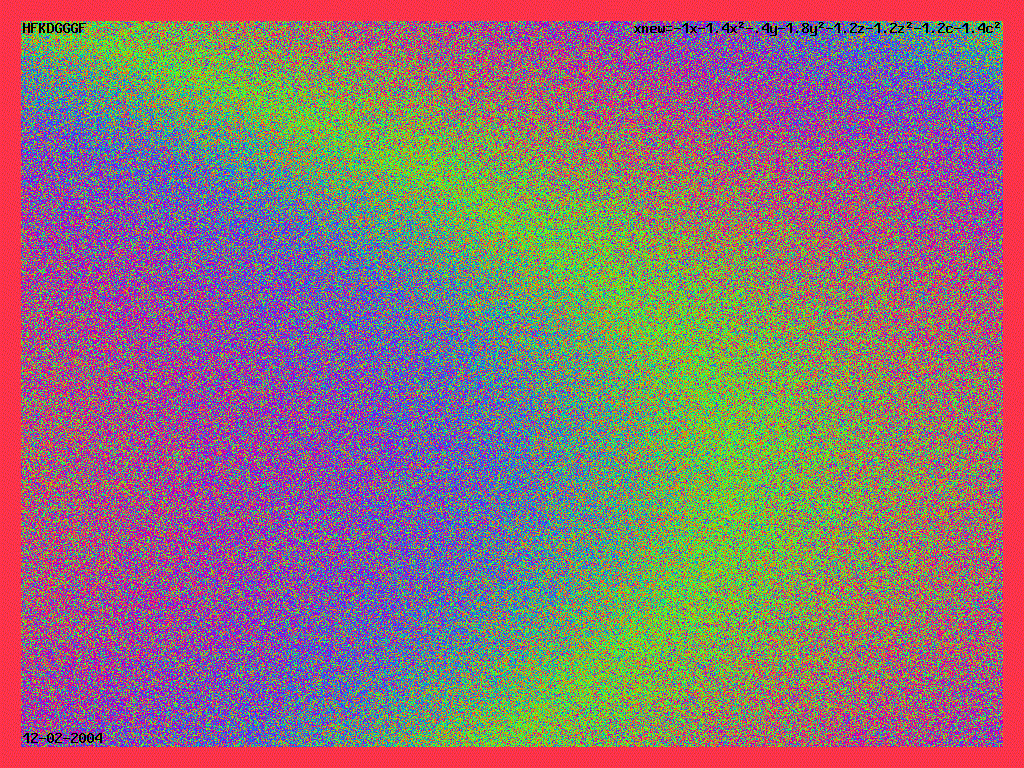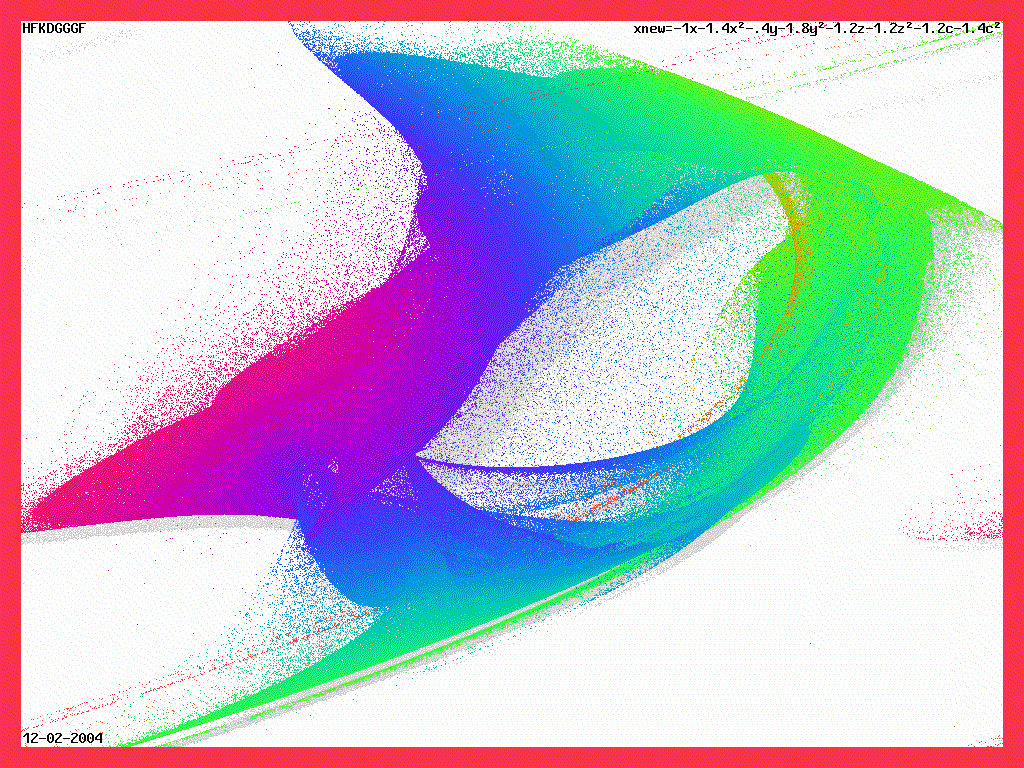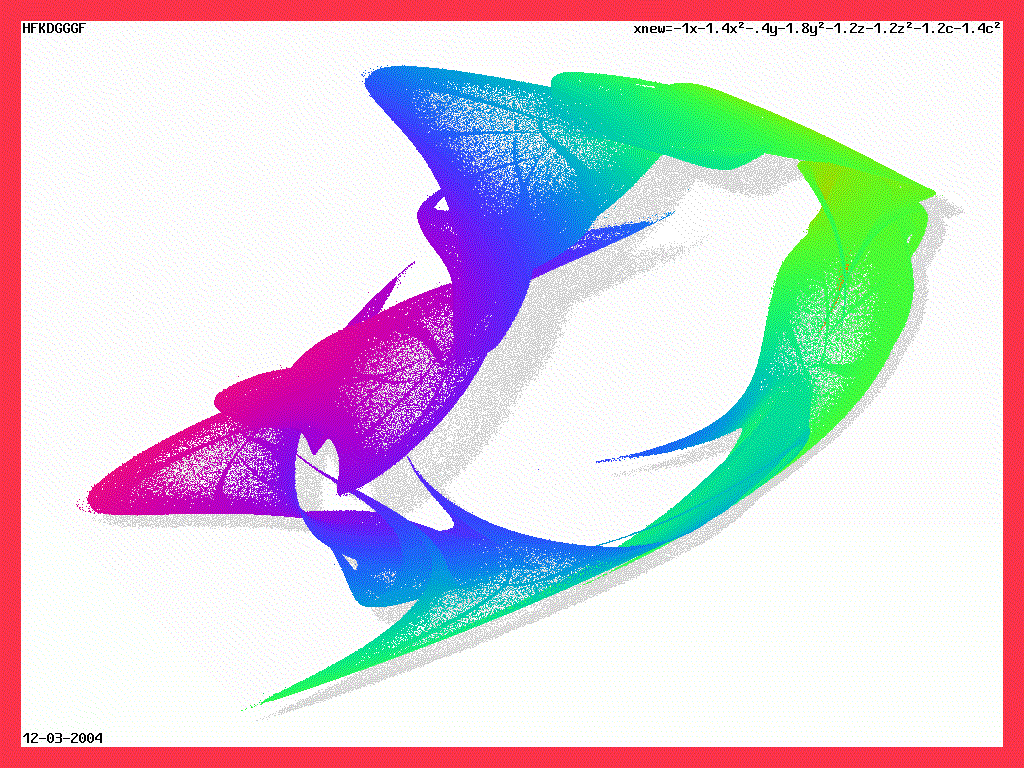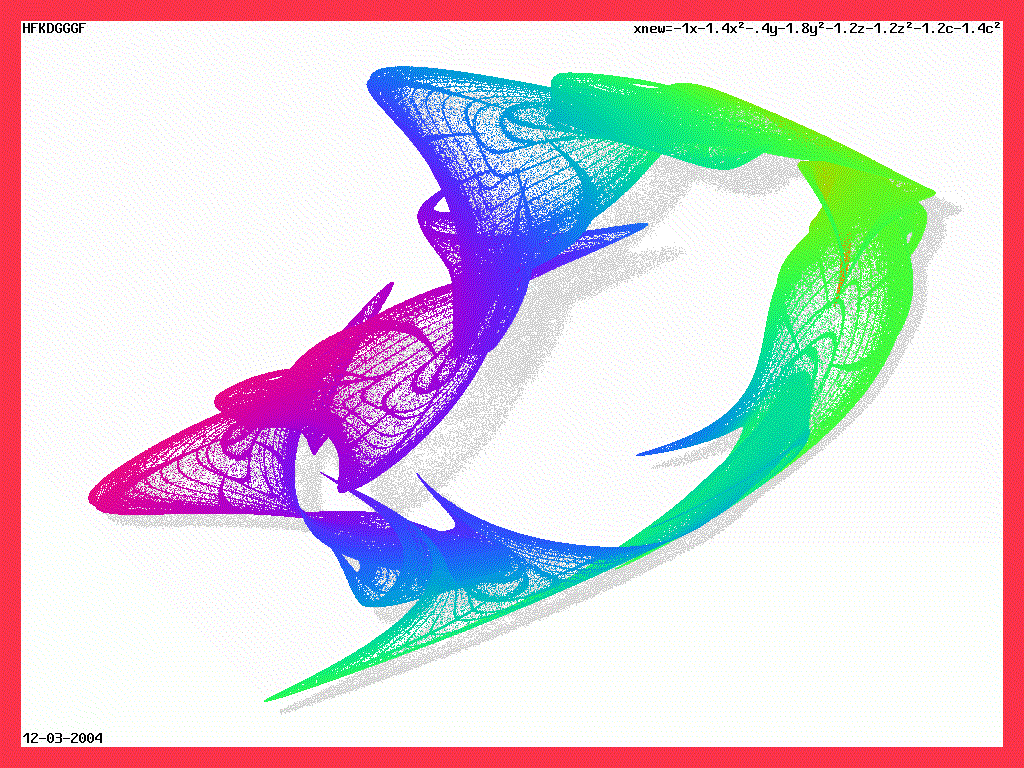











--------------
http://www.usenet-replayer.com/groups/a
http://alt.binaries.fractal-art.xus
http://sprott.physics.wisc.edu/
http://i.techrepublic.com.com/gallery/3
http://i.techrepublic.com.com/gallery/3
http://content.techrepublic.com.com/234
и далее http://content.techrepublic.com.com/234











--------------
http://www.usenet-replayer.com/groups/a
http://alt.binaries.fractal-art.xus
http://sprott.physics.wisc.edu/
http://i.techrepublic.com.com/gallery/3
http://i.techrepublic.com.com/gallery/3
http://content.techrepublic.com.com/234
и далее http://content.techrepublic.com.com/234

