|
|
Пишет schegloff (![[info]](http://lj.rossia.org/img/userinfo.gif){kind=small} schegloff)@ 2008-09-30 23:01:00 |
 |
|
 |
|
|
|
|
|
|
 |
|
 |
Холопский путь в СТО - 1, или Метод коэффициента К
Весной этого года я попросил у френд-ленты помощи в расчете самого обыкновенного полета на Альфу Центавра. К чести ЖЖ, нашелся человек -![[info]](http://lj.rossia.org/img/userinfo-lj.gif)
kaktus77@lj - который действительно помог мне кое-что посчитать. Однако результат этих расчетов оказался настолько своеобразным, что на том весь мой энтузиазм и закончился. Оказалось, что СТО (специальная теория относительности), при всей ее первоначальной очевидности, - дверь в интеллектуальную преисподнюю, из которой, насколько мне известно, еще никто не смог выбраться.
Как показали последующие месяцы, я слишком долго держал дверь открытой. Чем бы я ни занимался, в сознании постоянно зудел сверчок: "Ты перед СТО спасовал, а ведь это элементарная механика и школьная алгерба! Где уж тебе с более сложными задачами справиться!. Нуивот, я так больше не могу. Впереди планов громадье, и оставлять в тылу "пятую колонну" в виде СТО слишком рискованно. Попробую таки с ней разобраться, и прошу всех френдов, располагающих временем и квалификацией, мне в этом помочь. Сразу признаюсь - устраивающего меня решения задачи "Полет на Альфу Центавра" (равно как и других "парадоксов СТО") я все еще не нашел. Быть может, его удастся найти с вашей помощью; но куда вероятнее, что вековая тайна так и останется неразгаданной.
Начну с методического замечания. Что значит понять какую-либо теорию? На мой взгляд, для этого недостаточно заучить формулы и стандартные ответы на типовые вопросы. Понимать теорию значит уметь ей пользоваться, то есть решать с ее помощью задачи, а также уметь отличать ситуации, в которых теория работает, от ситуаций, в которых она неприменима. Поэтому далее я просто буду решать задачи. А там и посмотрим, решается ли задача "парадокс близнецов" в рамках СТО - или не решается.
Мир, в котором будут возникать наши задачи, предельно прост. Это плоская (одна пространственная и одна временная координаты) вселенная, в которой распространяются электромагнитные волны (свет и радио), а также летают с околосветовыми и постоянными скоростями звездолеты. На звездолетах имеются весьма качественные часы, обладающие 100% точностью хода, а также всевозможные средства связи. Каждому звездолету очень интересно, что происходит на других звездолетах, и его капитаны обращаются с соответствующими вопросами к корабельным теоретикам.
Движение звездолетов в нашем мире мы будем изображать на двумерных диаграммах Минковского: по горизонтали - пространственные координаты, по вертикали - временные. Неподвижный объект на таких графиках выглядит как вертикальный вектор (прет себе в будущее, не меняя расположения), а движущиеся - как наклоненные вправо или влево (куда движутся). В качестве единиц измерения используются единицы времени, расстояния меряются в пути, пройденном светом за эту единицу (например, световых секундах).
Задача первая. Мимо одного звездолета пролетает второй с относительной скоростью в 0.5с. Как звездолетам сверить часы, т.е. определить показания часов 1 и 2 в момент максимального сближения? Сам этот момент при скорости 0.5с пролетит - глазом моргнуть не успеешь. Кидаться друг в друга часами на 0.5с - уже военные действия. Поэтому обойдемся радиосигналами: пусть каждый звездолет посылает другому сигналы через равные промежутки времени:
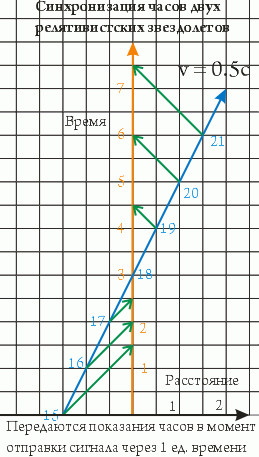
Равные они, как легко видеть, только с точки зрения посылающего звездолета. У принимающего звездолета интервал между принятыми сигналами будет сначала меньше, а потом, после максимального сближения - больше единицы. Момент, когда "меньше" превратится в "больше", и будет моментом максимального сближения, то есть синхронизации. В нашем случае такой момент наступает в точке 3 = 18. Промежутки времени между сигналами можно сделать достаточно малыми, так что и часы могут быть синхронизированы с достаточной для выявления неполадок в теориях точностью.
Задача вторая. Синхронизировав (взяв поправку -3 на одном звездолете и -18 на втором) часы в точке максимального сближения, звездолеты летят дальше по своим делам. Поскольку им интересна СТО, летят они не просто так, а продолжают обмен сигналами. Каждый звездолет посылает второму сигнал - "который час?", на который второй звездолет тут же отвечает - "столько-то!". Так вот, каким будет ответ второго звездолета на запрос, отправленный с первого через 1 единицу времени после синхронизации часов?
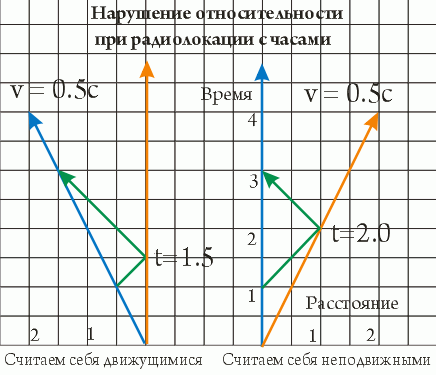
Нарисовав диаграмму, корабельный теоретик морщит лоб. Оказывается - смотря как считать. Для условно-движущегося звездолета один результат (1.5), для условно-неподвижного - другой (2.0). Перед тем как считать, надо сперва определить, какой из звездолетов движется "на самом деле", относительно неподвижного пространства ("светоносного эфира"). Например, отправив сигнал и посмотрев, каким будет ответ. Если 1.5 - мы движемся, если 2.0 - они движутся, если где-то между - движемся вместе. А пока теория бессильна...
Однако настоящему теоретику (такому, как Эйнштейн) подобный отказ от решения глубоко противен. Что это за теория, которая двух звездолетов связать не может? Попробуем немного поразмыслить. Звездолеты совершенно одинаковы? Ничего кроме них в нашем мире нет? Тогда относительно чего может двигаться звездолет "на самом деле"?! Быть может, результат нашего эксперимента окажется одинаковым в обоих случаях - хоть мы движемся, хоть стоим на месте?
Идея стоит того, чтобы ее проверить (как проверял свою безумную идею Лобачевский, пока из нее не выросла новая геометрия). Рисуем диаграмму с отметками промежутков времени (позаимствована из книги Г.Бонди, "Гипотезы и мифы в физической теории", с.40):
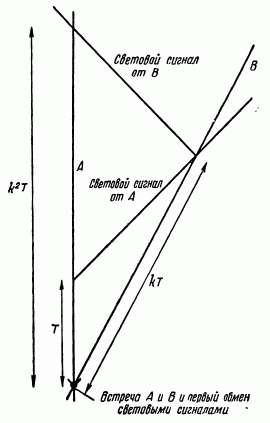
Пусть сигнал, отправленный в момент времени t, приходит на второй звездолет в момент k*t (вот он и появился, "коэффициент k"), где k - пока непонятно какой. Поскольку мы предположили, что оба звездолета равноправны, сигнал со второго звездолета, отправленный в момент t, также должен попасть на первый в момент k*t, а отправленный в момент k*t (приема сигнала с первого звездолета) - в момент k2*t.
Таким образом, сигнал, отправленный с первого звездолета в момент t, возвращается на него в момент k2*t. За этот промежуток времени свет успел слетать туда-обратно до точки встречи со вторым звездолетом, преодолев расстояние в k2*t - t (световых чего-то там). Поскольку мы считаем первый звездолет условно-неподвижным, расстояние "туда" рано расстоянию "оттуда", а момент отражения сигнала от второго звездолета - половине промежутка времени между отправкой и приемом сигнала = 1/2 * (t +k2*t). Получаем для момента отражения:
Tотр = 1/2 * (t +k2*t) = 1/2 * (k2+1)*t
Sотр =1/2 * (k2*t - t) = 1/2 * (k2-1)*t
Отсюда скорость "убегания" второго звездолета от первого:
v = Sотр / Tотр = (k2-1)*t / (k2+1)*t = (k2-1) / (k2+1)
Но поскольку скорость нам и так известна (эффект Допплера работает как часы), получаем отсюда формулу для самого коэффициента k (кому не лень, вспомните школьную алгебру и проделайте вывод самостоятельно):
k = SQRT( (1+v)/(1-v) ) (1)
Задача решена! Теперь теоретик может смело заявить капитану звездолета: сигнал, отправленный в 1.000 ед, вернется обратно с временем часов второго звездолета, равным 1.732 ед - независимо от того, считаем ли мы свой звездолет движущимся или неподвижным. Капитан конечно же спросит: а как так получается, что по нашим неподвижным часам у них там должно быть 2.000 ед - а у них только 1.732? Теоретик пожмет плечами и ответит: ну значит время в движущихся звездолетах идет как бы медленнее, и сразу посчитает, на сколько медленнее.
С точки зрения неподвижного звездолета, движущийся к моменту приема сигнала пролетел расстояние S = v * Tнеп, и то же самое расстояние сам сигнал прошел за S = 1 * (Tнеп - t), где t - момент отправки сигнала, а 1 - скорость света, которая у нас принята за 1. Отсюда:
Tнеп = t / (1-v)
По часам движущегося звездолета, как мы уже знаем, это будет k*t, то есть:
Tподв = t * SQRT( (1+v)/(1-v) )
Отсюда Tподв/Tнеп = SQRT( (1+v)/(1-v) ) * (1-v) = SQRT( (1+v) * (1-v) ) = SQRT (1 - v2) (2)
Мы с вами узнаем формулу Лоренца, и обреченно вздыхаем, понимая, что теоретика теперь уже ничем не пронять. Капитан об этом не знает, и делает последнюю попытку: ну хорошо, время у движущегося звездолета идет медленнее - а как насчет скорости? Если на расстоянии в 1 ед. у него не 2 ед. времени, а только 1.732 - значит, и скорость получается не 0.5, а целых 0.577?! Ну значит, отвечает на это теоретик, на движущемся корабле не только время замедляется, а еще и расстояния сокращаются - на тот же самый коэффициент. В результате скорость получится той же самой, а два варианта расчета радиолокации станут выглядеть вот так:
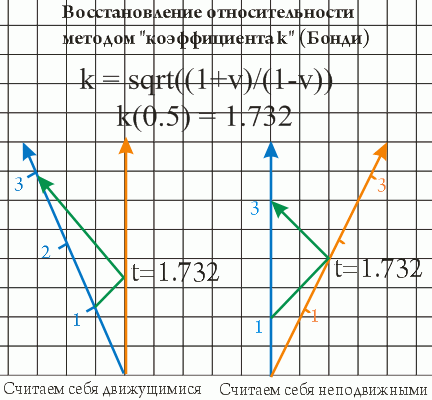
Полное торжество теории - как ни считай, а получается в обоих случаях одно и то же. Теоретик довольно скрещивает руки на груди. Капитан мрачно перекусывает сигару и задает каверзный вопрос: Так на каком из двух звездолетов на самом деле замедляется время? Теоретик пожимает плечами - ни на каком, звездолеты абсолютно равноправны. Да вы сами убедитесь - как раз световой день прошел с момента синхронизации, отправьте запрос на второй звездолет. Ставлю свой набор цветных карандашей против вашей треуголки, что в момент приема сигнала у них там будет 1.732 дня!
Ну уж нет, отвечает капитан. Я и сам подозреваю, что будет 1.732. Но вот как это получается? Не могу знать, отвечает теоретик. Как-то получается. Расчеты сходятся с экспериментом, чего ж вам еще надо? Разобраться, бормочет капитан, вытаскивая из коробки новую сигару. Вы пока можете идти, а я поколдую над чертежами. Чего-то в них определенно не хватает...
На этом заканчивается первая часть холопского пути в СТО. Формулы Лоренца выведены, теория торжествует. Но пройдет совсем немного времени, наш капитан звездолета додумается до парадокса часов, и все кончится очень плохо...
Продолжение следует
Весной этого года я попросил у френд-ленты помощи в расчете самого обыкновенного полета на Альфу Центавра. К чести ЖЖ, нашелся человек -
kaktus77@lj - который действительно помог мне кое-что посчитать. Однако результат этих расчетов оказался настолько своеобразным, что на том весь мой энтузиазм и закончился. Оказалось, что СТО (специальная теория относительности), при всей ее первоначальной очевидности, - дверь в интеллектуальную преисподнюю, из которой, насколько мне известно, еще никто не смог выбраться.Как показали последующие месяцы, я слишком долго держал дверь открытой. Чем бы я ни занимался, в сознании постоянно зудел сверчок: "Ты перед СТО спасовал, а ведь это элементарная механика и школьная алгерба! Где уж тебе с более сложными задачами справиться!. Нуивот, я так больше не могу. Впереди планов громадье, и оставлять в тылу "пятую колонну" в виде СТО слишком рискованно. Попробую таки с ней разобраться, и прошу всех френдов, располагающих временем и квалификацией, мне в этом помочь. Сразу признаюсь - устраивающего меня решения задачи "Полет на Альфу Центавра" (равно как и других "парадоксов СТО") я все еще не нашел. Быть может, его удастся найти с вашей помощью; но куда вероятнее, что вековая тайна так и останется неразгаданной.
Начну с методического замечания. Что значит понять какую-либо теорию? На мой взгляд, для этого недостаточно заучить формулы и стандартные ответы на типовые вопросы. Понимать теорию значит уметь ей пользоваться, то есть решать с ее помощью задачи, а также уметь отличать ситуации, в которых теория работает, от ситуаций, в которых она неприменима. Поэтому далее я просто буду решать задачи. А там и посмотрим, решается ли задача "парадокс близнецов" в рамках СТО - или не решается.
Мир, в котором будут возникать наши задачи, предельно прост. Это плоская (одна пространственная и одна временная координаты) вселенная, в которой распространяются электромагнитные волны (свет и радио), а также летают с околосветовыми и постоянными скоростями звездолеты. На звездолетах имеются весьма качественные часы, обладающие 100% точностью хода, а также всевозможные средства связи. Каждому звездолету очень интересно, что происходит на других звездолетах, и его капитаны обращаются с соответствующими вопросами к корабельным теоретикам.
Движение звездолетов в нашем мире мы будем изображать на двумерных диаграммах Минковского: по горизонтали - пространственные координаты, по вертикали - временные. Неподвижный объект на таких графиках выглядит как вертикальный вектор (прет себе в будущее, не меняя расположения), а движущиеся - как наклоненные вправо или влево (куда движутся). В качестве единиц измерения используются единицы времени, расстояния меряются в пути, пройденном светом за эту единицу (например, световых секундах).
Задача первая. Мимо одного звездолета пролетает второй с относительной скоростью в 0.5с. Как звездолетам сверить часы, т.е. определить показания часов 1 и 2 в момент максимального сближения? Сам этот момент при скорости 0.5с пролетит - глазом моргнуть не успеешь. Кидаться друг в друга часами на 0.5с - уже военные действия. Поэтому обойдемся радиосигналами: пусть каждый звездолет посылает другому сигналы через равные промежутки времени:
Равные они, как легко видеть, только с точки зрения посылающего звездолета. У принимающего звездолета интервал между принятыми сигналами будет сначала меньше, а потом, после максимального сближения - больше единицы. Момент, когда "меньше" превратится в "больше", и будет моментом максимального сближения, то есть синхронизации. В нашем случае такой момент наступает в точке 3 = 18. Промежутки времени между сигналами можно сделать достаточно малыми, так что и часы могут быть синхронизированы с достаточной для выявления неполадок в теориях точностью.
Задача вторая. Синхронизировав (взяв поправку -3 на одном звездолете и -18 на втором) часы в точке максимального сближения, звездолеты летят дальше по своим делам. Поскольку им интересна СТО, летят они не просто так, а продолжают обмен сигналами. Каждый звездолет посылает второму сигнал - "который час?", на который второй звездолет тут же отвечает - "столько-то!". Так вот, каким будет ответ второго звездолета на запрос, отправленный с первого через 1 единицу времени после синхронизации часов?
Нарисовав диаграмму, корабельный теоретик морщит лоб. Оказывается - смотря как считать. Для условно-движущегося звездолета один результат (1.5), для условно-неподвижного - другой (2.0). Перед тем как считать, надо сперва определить, какой из звездолетов движется "на самом деле", относительно неподвижного пространства ("светоносного эфира"). Например, отправив сигнал и посмотрев, каким будет ответ. Если 1.5 - мы движемся, если 2.0 - они движутся, если где-то между - движемся вместе. А пока теория бессильна...
Однако настоящему теоретику (такому, как Эйнштейн) подобный отказ от решения глубоко противен. Что это за теория, которая двух звездолетов связать не может? Попробуем немного поразмыслить. Звездолеты совершенно одинаковы? Ничего кроме них в нашем мире нет? Тогда относительно чего может двигаться звездолет "на самом деле"?! Быть может, результат нашего эксперимента окажется одинаковым в обоих случаях - хоть мы движемся, хоть стоим на месте?
Идея стоит того, чтобы ее проверить (как проверял свою безумную идею Лобачевский, пока из нее не выросла новая геометрия). Рисуем диаграмму с отметками промежутков времени (позаимствована из книги Г.Бонди, "Гипотезы и мифы в физической теории", с.40):
Пусть сигнал, отправленный в момент времени t, приходит на второй звездолет в момент k*t (вот он и появился, "коэффициент k"), где k - пока непонятно какой. Поскольку мы предположили, что оба звездолета равноправны, сигнал со второго звездолета, отправленный в момент t, также должен попасть на первый в момент k*t, а отправленный в момент k*t (приема сигнала с первого звездолета) - в момент k2*t.
Таким образом, сигнал, отправленный с первого звездолета в момент t, возвращается на него в момент k2*t. За этот промежуток времени свет успел слетать туда-обратно до точки встречи со вторым звездолетом, преодолев расстояние в k2*t - t (световых чего-то там). Поскольку мы считаем первый звездолет условно-неподвижным, расстояние "туда" рано расстоянию "оттуда", а момент отражения сигнала от второго звездолета - половине промежутка времени между отправкой и приемом сигнала = 1/2 * (t +k2*t). Получаем для момента отражения:
Tотр = 1/2 * (t +k2*t) = 1/2 * (k2+1)*t
Sотр =1/2 * (k2*t - t) = 1/2 * (k2-1)*t
Отсюда скорость "убегания" второго звездолета от первого:
v = Sотр / Tотр = (k2-1)*t / (k2+1)*t = (k2-1) / (k2+1)
Но поскольку скорость нам и так известна (эффект Допплера работает как часы), получаем отсюда формулу для самого коэффициента k (кому не лень, вспомните школьную алгебру и проделайте вывод самостоятельно):
k = SQRT( (1+v)/(1-v) ) (1)
Задача решена! Теперь теоретик может смело заявить капитану звездолета: сигнал, отправленный в 1.000 ед, вернется обратно с временем часов второго звездолета, равным 1.732 ед - независимо от того, считаем ли мы свой звездолет движущимся или неподвижным. Капитан конечно же спросит: а как так получается, что по нашим неподвижным часам у них там должно быть 2.000 ед - а у них только 1.732? Теоретик пожмет плечами и ответит: ну значит время в движущихся звездолетах идет как бы медленнее, и сразу посчитает, на сколько медленнее.
С точки зрения неподвижного звездолета, движущийся к моменту приема сигнала пролетел расстояние S = v * Tнеп, и то же самое расстояние сам сигнал прошел за S = 1 * (Tнеп - t), где t - момент отправки сигнала, а 1 - скорость света, которая у нас принята за 1. Отсюда:
Tнеп = t / (1-v)
По часам движущегося звездолета, как мы уже знаем, это будет k*t, то есть:
Tподв = t * SQRT( (1+v)/(1-v) )
Отсюда Tподв/Tнеп = SQRT( (1+v)/(1-v) ) * (1-v) = SQRT( (1+v) * (1-v) ) = SQRT (1 - v2) (2)
Мы с вами узнаем формулу Лоренца, и обреченно вздыхаем, понимая, что теоретика теперь уже ничем не пронять. Капитан об этом не знает, и делает последнюю попытку: ну хорошо, время у движущегося звездолета идет медленнее - а как насчет скорости? Если на расстоянии в 1 ед. у него не 2 ед. времени, а только 1.732 - значит, и скорость получается не 0.5, а целых 0.577?! Ну значит, отвечает на это теоретик, на движущемся корабле не только время замедляется, а еще и расстояния сокращаются - на тот же самый коэффициент. В результате скорость получится той же самой, а два варианта расчета радиолокации станут выглядеть вот так:
Полное торжество теории - как ни считай, а получается в обоих случаях одно и то же. Теоретик довольно скрещивает руки на груди. Капитан мрачно перекусывает сигару и задает каверзный вопрос: Так на каком из двух звездолетов на самом деле замедляется время? Теоретик пожимает плечами - ни на каком, звездолеты абсолютно равноправны. Да вы сами убедитесь - как раз световой день прошел с момента синхронизации, отправьте запрос на второй звездолет. Ставлю свой набор цветных карандашей против вашей треуголки, что в момент приема сигнала у них там будет 1.732 дня!
Ну уж нет, отвечает капитан. Я и сам подозреваю, что будет 1.732. Но вот как это получается? Не могу знать, отвечает теоретик. Как-то получается. Расчеты сходятся с экспериментом, чего ж вам еще надо? Разобраться, бормочет капитан, вытаскивая из коробки новую сигару. Вы пока можете идти, а я поколдую над чертежами. Чего-то в них определенно не хватает...
На этом заканчивается первая часть холопского пути в СТО. Формулы Лоренца выведены, теория торжествует. Но пройдет совсем немного времени, наш капитан звездолета додумается до парадокса часов, и все кончится очень плохо...
Продолжение следует
Добавить комментарий:
