Below are 25 friends' journal entries, after skipping by the 25 most recent ones.

[ << Previous 25 -- Next 25 >> ]

Wednesday, September 17th, 2025
lj_xaxam	5:38a	Предзнаменование Гладкий, толстый и жирный кролик Ёшкин кот Габи Айзенкотт решился бросить шляпу на ринг, опубликовав список своей партии под названием "Айзенкот без извилин". 120 имён, как положено: плох тот енерал, штаб которого не разработал планы полного разгрома всех противников. Не он первый, не он последний из генералов, обсиравшихся на политическом поле. Но в данном случае я случайно видел вблизи одного из его ближайших соратников. Маноло (Мануэля) Трахтенберга, считающийся израильским экономическим гением. Он как-то забрёл в наше профессорское кубло с лекцией "взгляд и нечто". Экономический гений при ближайшем рассмотрении оказался феерическим болваном и пустобрёхом, и после часа абсолютно пустопорожних словоизлияний (вопросов он попросил не задавать, чтобы не прерывать плавный поток его речи) я встал и демонстративно вышел, хлопнув дверью. Со мной вышли ещё несколько профессорьёв, торопившихся к своим делам. Сейчас я решил проверить свою память и посмотреть, чем отметился пустобрёх на разных высоких постах (он начал как назначенец Ольмерта, Биби сменил его как только выиграл выборы). ❝Был председателем национального совета по экономике при премьер-министре Израиля (2006–2009), где сыграл заметную роль в экономическом планировании страны. Возглавил правительственную социально-экономическую комиссию в 2011 году, чьи рекомендации легли в основу ключевых реформ после массовых социальных протестов против дороговизны жизни.❞ Комиссия Трахтенберга, созданная в результате "коттеджного протеста", родила мышь. Кажется, единственное, что частично удалось выполнить из его рекомендаций, — бесплатные детские сады для детишек моложе 3 лет. (В основном) на это ушло за три года около 60 ярдов шекелей (часть ушла на повышение пособий на аренду жилья для малоимущих). Всё так и оказалось. Долдон, пустое место, говорилла с докторской степенью. Зато Моня-Маноло точно знает, кто виноват. Такое знание дорого стоит. (Read Comments |Comment on this)
Tuesday, September 16th, 2025
lj_xaxam	5:47a	О должном Do your duty, come what may Я долго искал лаконичную формулировку того, как изменился наш мир (а особенно Ближний Восток) после чёрного дня 7 октября 2023 года. Дня, когда погибли 1200+ наших сограждан, и тусовщиков-make-love-not-war, и военных, включая беззащитных девочек-наблюдательниц, и киббуцников, долгие годы планировавших мирное сосуществование с соседями за несколько сотен метров, каковому сотрудничеству очень мешали назойливые многочасовые проверки соседей на блок-постах. Про "коньсепсию" я уж не буду вспоминать. В то страшное утро, пусть и не сразу, возродилась альтернативная коньсепсия, בעל הבית השתגע ("балабайт hиштагеа"). Перевод на русский язык непрост: "Хозяин {сошёл с ума, рехнулся, озверел, пошёл по стенке, охуел, ... } Выберите ваш вариант, а я попробую прояснить смысл. Израиль был крошкой-хаврошкой с 1948 года, когда какая-то шобла, преемница покойной Лиги Наций, выписала ему свидетельство о рождении. Не только ему, но и мертворождённому "Палестинскому государству". Никакой ультразвук тогда не смог выявить наличие органов, которые свидетельствовали бы о наличии сколько-нибудь жизнеспособного палестонского зародыша, казалось бы, в формалин — и в Кунсткамеру. Еврейский зародыш оказался вполне жизнеспособным, но немедленно встать на ноги и набить морду сразу всем супостатам, которые попытались было зародыша спустить в унитаз, не сумел. На долгие 19 лет, до Шестидневной войны, существовало шаткое равновесие между судорожно взрослевшим зародышем и дряхлеющими супостатами. И тут произошла Первая Смена Вех. Оказалось, мальчонка подрос и не просто научился постоять за себя, а ещё и доделал то, что не получилось сделать сразу после рождения. Понимание смены вех произошло не одномоментно и по-разному. Супостаты не утратили надежду на реванш, а интеллектуальные повивальные бабки, которые вначале любили зародыша как единственный жизнеспособный пример, подтверждающий их теорию о благотворном характере деколонизации на судьбе раскрепощённых туземцев, заподозрили нечистое и немедленно перевели зародыша из лиги успешно деколонизировавшихся аборигенов в лигу бастардов империализма и неоколонизаторов. Исключение было удачно исключено из теории, которая осталась без единственного "подтверждающего" примера. Ещё через шесть лет, аккурат в Судный день, драчливого подростка вызвали на пересдачу без подготовки, заставив отвечать довольно трудный билет. Подросток попотел, но справился как минимум на четыре с плюсом (некоторые поставили бы пять с минусом). После этого произошла Вторая Смена Вех. Подростку оформили аттестат зрелости и назначили responsible adult, "ответственным взрослым". В глазах всё тех же повивальных бабок-доброжелательниц это означало, что больше драться (даже до "первой юшки") ответственный взрослый не имеет никакого права. Да, он может иногда отшлёпать местную шпану, но делать это надо строго по Макаренко и Янушу Корчаку, выдавая строго дозированные воспитательные шлепки исключительно по мягким частям тела, чтобы упаси боже не нанести шпанёнку телесных повреждений. Новоназначенный Ответственный Взрослый взялся за дело ответственно. В Первую Ливанскую войну он шлёпнул хулигана Арафата так, что тот отлетел за кусты, аж в Тунис, но добивать его не стал. Меньше чем через десять лет, когда другой местный урка, Соддом Х., нарвался на полицейского и решил залупить из рогатки в Ответственного Взрослого в расчёте на то, что полицейский наряд разбежится в разные стороны и урке удастся улизнуть, Ответственный Взрослый ответственно сдержался, чтоб не отвлекать полицейских от их изначальной миссии. Урке удалось на какое-то время заховаться на малине, пока следующий наряд его там всё же не побрал. Казалось бы, можно было бы сказать, мол, свою миссию Ответственного Взрослого мальчонка выполнил с лихвой, но не тут-то было. Оказалось, что помимо заботы о порядке, в его обязанности входит ещё и воспитание трудного ребёнка, того самого сиротки, который (как казалось) не смог появиться на свет в 1948-м году. Смог, выходили. Этого сироту не только не полагалось шлёпать вообще: предполагалось, что Ответственный Взрослый возьмёт его себе в дом и даст ему ключи от всего на свете, начиная с холодильника и гаража, и кончая сейфом, где хранится табельное оружие. Сиротка быстро повзрослел и сообразил, в каком порядке пользоваться ключами. Дальнейшая история уже у всех на слуху: первая интифада, автобусный террор, террор самоубийц, вторая интифада, ... отделение от Газы, ракетные обстрелы из Газы, ... И всё это время все повивальные бабки, умиляясь резвости подросшего сиротки, водили хоровод вокруг Ответственного Взрослого и скандировали педагогические лозунги: шлёпни его за шалости, но не ремнём а ладошкой, лиши его мороженого на десерт, но полноценная горячая шварма чтоб была у него каждый день, отругай его как следует (лучше, когда мы отвернёмся ненадолго). И так продолжалось вплоть до самого чёрного дня. Когда резвый сорванец перерезал глотку ножом сыну Ответственного Взрослого, дочку изнасиловал, поджёг дом и уволок к себе в домик (в теоретико-игровом смысле, как в детских играх бывает) маму и бабушку. Повивальные бабки оцепенели от ужаса: ну как же так можно, это же нехорошо! Ну ладно, убитых уже не оживить, но маму с бабушкой верни, проказник! Иначе и мы тоже тебя отругаем! И тут-то балабайт hиштагеа, Ответственный Взрослый озверел. Всё, закрывайте ваш педсовет. Тот, кто порезвился у нас во дворе 7 октября, — не игривый шалун, которого можно отшлёпать как раньше было, — и воцарится так любезная вашему сердцу тишина. Нет. Это не люди, даже если среди них и есть грудные младенцы. За все годы эксперимента из этих ми-ми-мишных смуглых детишек никто не сумел вырастить никого, кроме садистов, насильников и убийц. А это означает, что хозяин-балабайт с этого момента (7 октября) делает то, что считает нужным. Отвечает ударом на удар, не слишком заморачиваясь соображениями пропорциональности, излишней заботой о возможной collateral damage. Слезинкой смуглого ребёнка пусть умывается тот, из-за кого этот ребёнок оказался в одном доме с архитеррористом. Иран нарвался в конце концов на сокрушительный удар по ядерной морде, решивши щёлкнуть балабайта по лбу залпом баллистических ракет "в знак солидарности с палестинским народом". Катар укрывал на своей территории преступников, признанных всем миром террористами. Недоукрыл, сейчас вот плачется о попранном суверенитете утраченной семейной чести. Но балабайту плевать на повивальных бабок, которые сердито брюзжат на лавочке, побрюзжат — перестанут. Fac quod debes, fiat quod fiet. Делай что должно, и будь что будет. Ничего особенного не случится, впрочем. (Read Comments |Comment on this)
lj_xaxam	5:06a	Подсчёт убытков Суперспарта С утра интернеты и радиоканалы лопаются от вчерашней "суперспартанской" речи Биби. Уже пошли сравнения Израиля с Северной Кореей... Я задал Перплешке два вопроса: на какую сумму Израиль закупает вооружений (а речь идёт именно об автаркизации израильского военпрома) в странах Европы, и каков общий бюджет нашего министерства обороны на закупку вооружений (включая внутренние закупки). Ответы: примерно на 400 мегабаксов в год мы закупаемся в Европе, а общие затраты — порядка 35 ярдов баксов. Гроша на эти же вопросы даёт ответы 1 ярд и 30 ярдов соответственно. Кто правее — в общем, не слишком важно, порядок примерно тот же. Чтобы восполнить возможное европейское эмбарго на поставки оружия, надо напрячься и увеличить внутреннее производство вооружений на астрономические один-два-три процента. Для сравнения: "естественный" годовой прирост ВВП Израиля — как раз примерно 3.5% (а перед войной был вообще 6%!). Я не хочу сказать, что ЦАХАЛь не заметит европейского эмбарго. Заметит. Но катастрофой оно не станет. Кроме того, надобно более внимательно смотреть, какие конкретно страны и какое именно вооружение сейчас продают Израилю. Скажем, Германия строит дорогущие подлодки, и будет последней в ряду стран, вводящих эмбарго (if at all). Несколько лет без новых подлодок Израиль перекантуется как-нибудь, а в предыдущем уравнении краткосрочный "ущерб" от эмбарго будет ещё меньше. (Read Comments |Comment on this)
Monday, September 15th, 2025
syn_trv_science	4:17p	Зрение человека, животных и машин. Жизнь и работы Вадима Максимова Публикуем воспоминания Елены Михайловны Максимовой, вед. науч. сотр. Института проблем передачи информации РАН, о ее супруге Вадиме Викторовиче Максимове (26.08.1937–14.04.2015), ярком представителе отечественной школы сенсорной физиологии, воспитаннике МФТИ, ученике и последователе Михаила Бонгарда. См. также тексты Олега Юрьевича Орлова о Вадиме Викторовиче, опубликованные в ТрВ-Наука и на сайте ИППИ РАН. Сообщение Зрение человека, животных и машин. Жизнь и работы Вадима Максимова появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	3:04p	Красота самоопирающихся конструкций Одна из моих любимых тем — отношения «камень, ножницы, бумага», встречающиеся в разных областях: математике, биологии, социальных науках и др. Напомню, что в одноименной игре камень доминирует над ножницами, ножницы — над бумагой, бумага — над камнем; но так бывает не только в играх, этот тип отношений встречается в самых разных областях. Сообщение Красота самоопирающихся конструкций появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	3:04p	Психология и только психология. Рассказ Павла Амнуэля Сегодня в изломанной линии крыш Чикаго, как ей показалось, ничего не изменилось. Как каждый день, даже в воскресенье, когда в университете не было лекций, она села на широкую каменную скамью, уже прогретую солнцем — хотя и осенним, но всё еще теплым. Она сидела, подставив лицо солнечным лучам, закрыв глаза, и думала — о студентах, об удачной или неудачной лекции, о статье, почти уже законченной. Чья-то тень загородила от нее солнце, она открыла глаза и увидела, что перед ней стоит высокий мужчина с темно-каштановыми волосами, в светлой рубашке — и разглядывает ее с явным интересом… Сообщение Психология и только психология. Рассказ Павла Амнуэля появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	1:02p	Про переименования Между прочим, обладательницу белейшей веснушчатой кожи, рыжеволосую девочку Юлю интеллигентные родители послали летом отдохнуть в детский оздоровительный центр. Это то, что раньше именовалось пионерским лагерем. Вернувшись оттуда, счастливая Юля стала делиться чудесными впечатлениями о тамошней жизни. И в речке купалась до синевы в губах, и в волейбол до упаду играла, а в конкурсе «Что? Где? Когда?» заняла второе место. Здорово, правда? Напоследок решила поделиться с отцом и вновь приобретенным сакральным знанием… Сообщение Про переименования появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	12:33p	Перевод с вещи на вещь Расширяя лингвистическую теорию перевода: не только слова и образы, но и вещи и обстоятельства. Культурологи Александр Марков и Оксана Штайн рассматривают мастерскую Рембрандта как полигон расширенного перевода, включающего сами вещи, а не только их языковые отображения. Сообщение Перевод с вещи на вещь появились сначала на Троицкий вариант — Наука. (Comment on this)
Sunday, September 14th, 2025
syn_trv_science	4:15p	«Знание» — сила Продолжение цикла воспоминаний Михаила Михайлова из его будущей книги «Как я был ученым». Предыдущие публикации: https://www.trv-science.ru/tag/mihail-mihajlov/ Сообщение «Знание» — сила появились сначала на Троицкий вариант — Наука. (Comment on this)
tiphareth	3:09p	One chromosome too many "Юмор" типа https://babylonbee.com/news/universities-quietly-cancel-kill-conservatives-101-courses Universities Quietly Cancel 'Kill Conservatives 101' Courses https://babylonbee.com/news/democrats-say-theres-no-place-for-violence-against-evil-nazi-republicans-that-are-literally-killing-people-and-destroying-america Democrats Say There's No Place For Violence Against Evil Nazi Republicans That Are Literally Killing People And Destroying America Не то чтобы смешно, но отчасти метко, в штатах гуманитарные курсы это примерно как "история КПСС" при советской власти, там тоже не учат ничему, кроме промывания мозгов. Не все, может, но точно больше половины. Что характерно (и я это знаю от знакомых профессоров, типа от первых рук), даже в топовых университетах домашки по гуманитарным курсам делаются сейчас строго через AI, вообще никакого другого способа написать еженедельное эссе по гуманитарной дисциплине студенты не видят. То есть по сути студентов давно автоматизировали. Можно было бы, конечно, автоматизировать и профессоров, но проще, думаю, просто закрыть все гуманитарные факультеты в университетах. Конечно, какое-то количество приличных людей окажутся без работы, но (а) там ничему не учат, и уже никогда ничему не будут учить, однако LLM запретить не получится; а LLM делает работу гуманитарного студента лучше, чем студент, уже сейчас; и (б) все эти люди неиллюзорно социально опасны. В принципе, еще лет 5, и LLM будет делать домашки по естественным наукам ничуть не хуже, но как с этим бороться, мы уже понимаем, а решения аналогичной задачи в гуманитарных науках нет, и не будет, видимо. Вот хорошее https://www.tabletmag.com/contributors/sergiu-klainerman собрание статей знаменитого математика Сержиу Клейнермана об ужасах SJW в высшем образовании. Особенно вот: https://www.tabletmag.com/sections/arts-letters/articles/academic-administrators-strangling-universities рассказывает, что за последние 20 лет власть университетских администраторов сделалась абсолютной, а их численность и количество ресурсов, которые они потребляют, удваивается каждые 10-20 лет, в итоге сейчас в топовых университетах больше администраторов, чем собственно студентов; при этом, численность профессоров и их прокорм не увеличивается с начала 1990-х, и итоге университеты превратились в места, где административные работники (с дипломами гуманитарных факультетов) заняты промыванием мозгов студентам, а функция профессора - молчать в тряпочку во избежание санкций и увольнения. Думаю, что пиздец, который наступил в Америке, это результат подобной эволюции университетов и только, то есть падение науки, особенно гуманитарной, было основной причиной, почему обе партии, конгресс, сенат, корпоративные масс-медиа и судейская система в Штатах в подобном упадке, а президентами от раза к разу выбирают полных даунов, вдесятеро глупее, чем типа рандомный мудак с улицы. https://www.youtube.com/watch?v=gpnrfYA4aWQ Mongoloid Mongoloid, he was a mongoloid Happier than you and me Mongoloid, he was a mongoloid And it determined what he could see Mongoloid, he was a mongoloid One chromosome too many Mongoloid, he was a mongoloid And it determined what he could see And he wore a hat And he had a job And he brought home the bacon So that no one knew He was a mongoloid, mongoloid His friends were unaware Mongoloid, he was a mongoloid Nobody even cared Mongoloid, he was a mongoloid One chromosome too many Mongoloid, he was a mongoloid And it determined what he could see And he wore a hat And he had a job And he brought home the bacon So that no one knew He was a mongoloid, mongoloid Happier than you and me Mongoloid, he was a mongoloid And it determined what he could see Mongoloid, he was a mongoloid One chromosome too many Mongoloid, he was a mongoloid And it determined what he could see And he wore a hat And he had a job And he brought home the bacon So that no one knew Mongoloid, he was a mongoloid * * * Привет Current Mood: sick Current Music: Devo - The Truth About De-Evolution (309 Comments |Comment on this)
syn_trv_science	3:01p	Гейзенберг, Борн, Паули — кто больший осёл? Революционную работу Вернера Гейзенберга 1925 года «О квантовотеоретическом истолковании кинематических и механических соотношений» (Heisenberg, 1925) сразу признали физики, с которыми он тесно общался. Макс Борн с первого взгляда оценил прорыв своего ассистента и сам немедленно приступил к развитию его идеи. Так же поступил и молодой англичанин Поль Дирак, к которому рукопись Гейзенберга тоже попала еще до выхода статьи в свет. Нильс Бор, выступая в конце августа 1925 года на шестом Скандинавском математическом конгрессе, оценил первую статью Гейзенберга как выдающееся достижение. Однако большинству физиков статья Гейзенберга показалась не очень важной или осталась непонятной… Сообщение Гейзенберг, Борн, Паули — кто больший осёл? появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	3:01p	От партизана до математика Этой весной архив Центра «Холокост» пополнился богатой коллекцией личных документов Якова Марковича Каждана — ученого-математика, участника Великой Отечественной войны. Это многочисленные семейные и фронтовые фотографии; письмо его друга военной поры — сбитого под Белгородом летчика; важные свидетельства эпохи послевоенного времени. Яков Маркович приходится мне родным — он дедушка моего двоюродного брата, свекр покойной тети Ларисы Любарской. Повествование об этой яркой, незаурядной личности, несомненно, заслуживает читательского внимания. Сообщение От партизана до математика появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	1:49p	Семь летних дней в НИИЧАВО Еще один научный институт появился в конце августа в наукограде Троицке. Правда, всего на неделю — в «Байтике» 1, как сообщала табличка перед входом, открылся филиал НИИЧАВО РАН. Открылся как раз вовремя — мир отмечает 100-летие Аркадия Стругацкого, одного из авторов легендарной повести «Понедельник начинается в субботу», действие которой и происходит в НИИЧАВО. Сообщение Семь летних дней в НИИЧАВО появились сначала на Троицкий вариант — Наука. (Comment on this)
tiphareth	11:31a	better dead than russian А по поводу "бусификации", не знаю уж, есть она или это фикция, изобретенная лахтоботами. Но точно знаю, что лучше быть мертвым, чем русским. Так что тащите все, бусификация не бусификация, разницы никакой. Лучше быть мертвым, чем русским. В степи, покрытой пылью бренной, Сидел и плакал человек, А мимо шёл Творец Вселенной. Остановившись, он изрек: ``Я друг униженных и бедных, Я всех убогих берегу. Я знаю много слов заветных. Я есмь твой Бог. Я всё могу. Меня печалит вид твой грустный - Какой нуждою ты тесним? И человек сказал: ``Я русский''. И Бог заплакал вместе с ним. Привет Current Mood: sick Current Music: Lacrimosa - STILLE (183 Comments |Comment on this)
tiphareth	10:56a	"Charlie Kirk was a christofascist scumbag and the world is a better place without him being in it. Good riddance." Смешно https://stas.dreamwidth.org/1486819.html либералы веселятся, что трансы убили кристофашистского говноеда, а гопы бьются в лицемерной истерике, что пол-твиттера прыгают от радости, что того убили. Не понимаю, что тут плохого. Вот если бы убили, например, опру, или рэчел медоу, или дон-лимона, или вообще любого из партийных говноедов, не вылезающих из зомбоящика - неужели кто-нибудь из этих лицемеров огорчился бы? кирк был говно, лицемерное и безголовое, причем целиком улегся под путлера, как и половина гоп-партии. Но даже среди гопов, улегшихся под путлера, есть менее мерзкие люди, а этот был какой-то совсем конченый. Это, конечно, не повод праздновать очередное достижение ебанутых трансов, нахуй вообще, в итоге будет как с поджогом рейстага, гопы закрутят гайки по полной, причем демы, когда одолеют гопов, ничего откручивать не станут, конечно, одна партия другой стоит. В общем, нет никакой радости в том, что тушка очередного безмозглого говноеда покинула сей мир, подобного говнища в мире миллиарды, девать некуда. Но уж огорчаться по этому поводу совсем глупо. Но проблема не в том. Убивайте хоть Соловьева, хоть Собчак, хоть Яшина с Быковым или Волковым, с обоих сторон любой политической движухи говна столько, что и лопатой не выгребешь. Проблема не в том, что какое-то говно убили, проблема в том, что очередное убийство вызывает chilling effect, людишки (и без того подлые, лживые и трусливые) делаются еще подлее, лживее и трусливее, если видят, что рядом началось мочилово. Апропос: Консервапедия, англоязычный проект для гопов, которых випиздили из Википедии за нарушение либерального консенсуса, превратилась в коллекцию ссылок на кремлевскую пропаганду https://www.conservapedia.com/Volodymyr_Zelensky https://www.conservapedia.com/Vladimir_Putin https://www.conservapedia.com/Russian_sanctions https://www.conservapedia.com/Maidan_coup https://www.conservapedia.com/Background_of_the_Russia-Ukraine_war https://www.conservapedia.com/NATO_war_in_Ukraine https://www.conservapedia.com/Ukraine Даже на русском подобное хуй найдешь, граждане религиозно компилируют высеры лахтоботов, и превратили продукцию рт.ком в символ веры, сияющий на небе по соседству с ликом великого Дональда. Гопы реальне ебанутые, даже если сравнивать с SJW-активистами, непонятно, кто хуже. Привет Current Mood: sick Current Music: Lacrimosa - STILLE (43 Comments |Comment on this)
Saturday, September 13th, 2025
syn_trv_science	9:03p	Милосердие и человечность Еще в начале 1960-х годов братья Стругацкие, создав впечатляющий образ мира Полудня, мира, в котором им самим хотелось бы жить, задумались о том, как этот мир мог бы возникнуть из нашего реального? Активно продвигая тезис «почти такие же, как мы», населяя мир Полудня лучшими из своих современников, писатели поначалу думали, что этот гипотетический мир может возникнуть простым переходом количества в качество. Мол, число «правильных» людей будет расти, и они неизбежно станут абсолютным большинством. Увы, довольно скоро эйфория оттепели сменилась скепсисом: а с чего бы это изменения в поведении людей будут идти именно в правильном направлении? Да полно, существенно ли изменилось поведение отдельной личности за последние две тысячи лет? Стало ясно, что процесс «улучшения» общества нужно подталкивать. Писателей стали занимать вопросы: что для этого нужно делать, кто этим будет заниматься, как это будет происходить? Сообщение Милосердие и человечность появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	9:03p	Календарь фантастики: Аркадий Стругацкий, Эдгар Берроуз, Антон Молчанов, Андрей Петров, Валентин Гафт, Артур Кёстлер, Александр Куприн, Александр Хмелик 100 лет назад родился Аркадий Натанович Стругацкий (С. Бережков, С. Ярославцев, 1925–1991), русский писатель. 150 лет назад родился Эдгар Райс Берроуз (Нормал Бин) — Edgar Rice Burroughs (Normal Bean, 1875–1950), американский писатель, автор сериалов о Джоне Картере на Марсе, Карсоне Нэпьере на Венере, эпопеи о Тарзане Великолепном, о подземной стране Пеллюсидар. 65 лет назад родился Антон Викторович Молчанов (Ант Скаландис, р. 1960), русский писатель, автор романов «Катализ», «Заговор Посвященных», «Меч Тристана», циклов «Наемные самоубийцы», «Ненормальная планета», «Причастные», «Мир Смерти» (с Гарри Гаррисоном), книги «Братья Стругацкие». 95 лет назад родился Андрей Павлович Петров (1930–2006), русский композитор, автор оперы-феерии «Маяковский начинается», балетов «Сотворение мира», «Мастер и Маргарита», симфонической фантазии «Синяя птица», музыки к спектаклям «Бегущая по волнам», «Жизнь Сент-Экзюпери», «Легенда об Уленшпигеле», «Гамлет», кинофильмам «Человек-амфибия», «Тридцать три», «Его звали Роберт», «Старая, старая сказка», «Синяя птица», «Веселое сновидение, или Смех и слезы», «Небеса обетованные», «Настя», «Предсказание». 90 лет назад родился Валентин Иосифович Гафт (1935–2020), российский актер, исполнитель ролей в кинофильмах «Калиф-аист» (Кашнур-волшебник), «Удивительный мальчик» (Доктор Капа), «Заговор» (Кейси), «Иван да Марья» (Казначей), «Короли и капуста» (Фрэнк Гудвин), «Черная курица, или Подземные жители» (Дефорж, учитель французского / Король), «Чародеи» (Аполлон Митрофанович Сатанеев), «Про кота…» (Людоед), «Забытая мелодия для флейты» (Одиноков, чиновник Главного управления свободного времени), «Время летать» (Виктор), «Небеса обетованные» (Дмитрий Логинов, предводитель бомжей), «Мастер и Маргарита» (1994, Воланд), «По ту сторону волков» (Игорь Алексеевич Голощёков, врач), «Девять неизвестных» (Виктор Севидов, миллиардер), «Мастер и Маргарита» (2005, Каифа / Человек во френче), «Книга мастеров» (Волшебное зеркало), «Млечный Путь» (Шаман). 120 лет назад родился Артур Кёстлер (Arthur Koestler, 1905–1983), английский писатель и журналист, автор романов «Мрак в полдень» («Слепящая тьма»), «Век Вожделения», философских эссе «Сомнамбулы», «Акт творения», «Призрак из машины», пьесы «Полуночный бар». 155 лет назад родился Александр Иванович Куприн (1870–1938), русский писатель, автор повестей «Жидкое солнце», «Звезда Соломона», рассказов «Тост», «Королевский парк», «Механическое правосудие». 100 лет назад родился Александр Григорьевич Хмелик (1925–2001), русский драматург и сценарист, автор пьесы «А все-таки она вертится?.. или Гуманоид в небе мчится», сценариев к кинофильмам «Два дня чудес», «Иван да Марья», «Новые приключения капитана Врунгеля», «Если верить Лопотухину…», «На златом крыльце сидели…». Сообщение Календарь фантастики: Аркадий Стругацкий, Эдгар Берроуз, Антон Молчанов, Андрей Петров, Валентин Гафт, Артур Кёстлер, Александр Куприн, Александр Хмелик появились сначала на Троицкий вариант — Наука. (Comment on this)
syn_trv_science	5:30p	Астроновости: твердое ядро Марса, молодые звезды в М96, землеподобные планеты у TOI‑2322, лунное затмение… Сравнение внутренних структур Земли и Марса показывает, что Красная планета, подобно Земле, состоит из коры, мантии и ядра. Анализ сейсмических данных посадочного аппарата NASA InSight выявил, что ядро Марса состоит из твердого внутреннего ядра радиусом около 613 ± 67 км и жидкой металлической оболочки (внешнего ядра) радиусом примерно 1800 км. Статья об исследовании внутреннего строения нашего соседа была опубликована в журнале Nature. Космический телескоп «Хаббл» предоставил новое инфракрасно-оптическое изображение галактики M96, расположенной на расстоянии около 35 млн световых лет от нас в созвездии Льва. Она отличается асимметричной структурой со смещенным относительно центра ядром и витиеватыми спиральными рукавами. Эти особенности, вероятнее всего, объясняются гравитационным взаимодействием с соседними галактиками, способствовавшим такому распределению газа и пыли с неравномерной плотностью, что вызвало истончение структуры на отдельных участках диска. Кассиопея A — один из наиболее изученных остатков сверхновой, образовавшейся при коллапсе массивной звезды более 300 лет назад. Новое исследование на основе данных космической рентгеновской обсерватории «Чандра» показало, что за несколько часов до взрыва внутренние слои звезды претерпели резкую перестройку. Результаты были опубликованы в журнале The Astrophysical Journal. На основе наблюдений космического телескопа TESS и последующих спектроскопических измерений выявлена система из двух транзитных экзопланет, обращающихся вокруг звезды TOI-2322. Первая планета, TOI-2322 b, по параметрам сравнима с Землей, хотя и обращается по орбите периодом около 11,3 суток, а ее масса, по оценкам, меньше двух земных масс. Вторая, TOI-2322 c, обладает радиусом почти в 1,9 земного, но массой порядка 18 земных, что говорит о ее крайне высокой плотности (около 14,7 г/см³) и позволяет отнести к числу самых массивных «суперземель», чья предполагаемая внутренняя структура сходна с нашей планетой. В ночь с 7 на 8 сентября жители разных уголков планеты стали свидетелями зрелищного астрономического явления — полного лунного затмения. Особенностью этого затмения стало то, что Луна оказалась очень близко к центру тени Земли, что привело к более сильному затемнению северной части ее диска. В тени спутник нашей планеты пребывал 1 час 22 минуты, с 20:31 до 21:53 мск. Изображение номера: вращающийся пульсар в Крабовидной туманности. Сообщение Астроновости: твердое ядро Марса, молодые звезды в М96, землеподобные планеты у TOI‑2322, лунное затмение… появились сначала на Троицкий вариант — Наука. (Comment on this)
lj_xaxam	2:31p	Врёт, как адвокат Увёртливый, сучок У Толи avva в обсуждении замечательных задачек Вити Прасолова для школьников возникла дискуссия по поводу одной из задач, про фонари, освещающие дорожку в парке. С математической точки зрения речь идёт о следующем утверждении. Выпуклое компактное множество К на одномерной прямой ℝ покрыто несколькими одномерными открытыми связными подмножествами (интервалы, лучи, вся прямая). При этом некоторые точки неизбежно (почему?) оказываются покрытыми несколько раз, минимум дважды. Надо доказать, что из исходного покрытия можно выбрать подпокрытие так, чтобы любая точка оказалась покрытой не более чем двумя из оставшихся неотброшенными множеств. (Подразумевается, что каждый фонарь освещает выпуклое множество одномерной дорожки: видевшие иные фонари приглашаются в бан). Задача очевидным (для геометров) образом является одномерным случаем следующей задачи. В Евклидовом аффинном n-мерном пространстве компактное множество X покрыто выпуклыми открытыми множествами. Каждая точка x ∈ X тем самым покрыта не менее чем nx ≥ 1 раз. Требуется доказать, что исходное покрытие можно проредить, выкинув из него часть покрышек, так, чтобы остающиеся покрышки (а) всё ещё покрывали X целиком, и (2) ни одна точка не была покрыта более чем n + 1 покрышкой. При n = 1 имеем ровно задачу Вити Прасолова для школьников. Для причастных к математике я осмелюсь напомнить — это отнюдь не первое подобное утверждение. Наиболее близкие "по духу" — теоремы Хелли и Каратеодори (обе относятся к началу 20 века), будут запросы, расскажу. Но с выше сформулированной задачей — оказалась какая-то засада. Меня математике учили в Маскве, а результат, указанный выше, ИИ (Перплешка) приписывает Данилычу, питерскому титану Александру Даниловичу Александрову. Он ушёл в 1999-м, я мог бы ещё при желании поговорить с великим человеком, но пришлось ограничиться контактами через одно рукопожатие (Залгаллер, Канторович, Мнёв, ... ). Но откуда-то из эманаций я знал про этот его результат, который немедленно вспомнил, глядя на задачу Вити Прасолова. Где я про него прочитал, будучи ещё студентом, сейчас вспомнить не могу: ни тогда, ни сейчас это не был фокус моих математических интересов. Так, боковое зрение, желание быть в курсе того, о чём думают коллеги. Но у меня ни секунды не было сомнений, что сформулированный выше результат про выпуклые покрытия — правильный и в самом деле скорее всего принадлежит Данилычу. Дело в том, что он (результат) прекрасно вписывается в теорию размерности Лебега-Гуревича, которая определяет размерность абстрактных топологических пространств, не вложенных ни в какое евклидово пространство ℝⁿ, через комбинаторику их покрытий. Общая конструкция примерно та же самая: рассматриваем всевозможные покрытия топологического пространства Х и пытаемся их проредить, насколько можно, выкинув как можно больше покрышек, при этом следя за тем, какое максимальное число раз будут покрыты разные точки Х (это число называется кратностью покрытия). Результат, конечно, зависит от изначального покрытия (например, если оно состояло всего из одной гигантской покрышки, то ничего выкидывать не надо, и кратность будет единицей). Но нас интересует наихудший вариант, скажем, когда исходное покрытие состоит из очень маленьких открытых покрышек (возможно, в бесконечном числе), — насколько сильно его можно проредить? Лебег, Куратовский и Гуревич разбирали эту задачу и сформулировали условия, при которых существует конечное число N такое, что из любого открытого покрытия можно вычленить подпокрытие кратности не больше N. В этом случае есть все основания называть число N − 1 размерностью топологического пространства Х. Надо ли упоминать отдельно, что размерность по Лебегу-Гуревичу монотонна, подмножество в ℝⁿ не может иметь размерность больше n? Общая топологическая теория изобилует техническими сложностями. Но если мы живём в аффинном (например, евклидовом) пространстве, то там определено понятие выпуклых множеств: множество Х называется выпуклым, если вместе с каждыми своими двумя точками x,y ∈ X оно содержит весь отрезок [x,y]. Сама по себе выпуклость не гарантирует открытость множества Х, но если уж оно открыто, то его топология тривиальна (как у открытого шара), поэтому большинство технических условий в теории Лебега-Гуревича должны быть выполнены автоматически, если все покрышки выпуклы и открыты. А Данилыч был, несомненно, одним из самых выпуклых геометров двадцатого века. Кароче. задав чиста канкретный математический вопрос Перплешке и получив в ответ чиста канкретный ответ, я ни на секунду не усомнился и отписал этот ответ у Аввы. О чём сейчас искренне жалею. Дальнейшее будет интересно в основном дрессировщикам ИИ.  Интересующимся математикой вопроса я обязуюсь ответить в меру своей малоосведомлённости. Полюбуйтесь. Мы с Перплешкой, начиная с третьей итерации,  буквально начали друг друга матюгами крыть: он вертелся вьюном на горячей сковородке, врал в каждом конкретном ответе, но так и не нашёл конкретной ссылки на тот лаконичный результат, которым он начал нашу беседу. Я уже знаю, что ИИ страшно не любит, когда его держат за поисковика-ищейку, но я попытался его припереть к стенке. Безуспешно. Уворчаивается, сучок. Предлагаю коллегам-математикам челлендж. Заставьте ваших дрессированных ИИ найти ближайшее приближение к "лемме Александрова" (цитированной выше). Нашедший контрпример к этой формулировке получит приз: я тому богатырю двух лягушек подарю и еловую шишку пожалую™. Последам Помрачение какое-то! Конечно, утверждение о кратности неверно даже на плоскости. Вот простейший пример (спасибо alevaj и delta_4). За лягушками и шишкой обращайтесь в редакцию "ХВ"! Возьмём единичный квадрат и покроем его четырьмя маленькими квадратиками со стороной чуть больше половины с центрами в вершинах большого квадрата. Центр большого квадрата будет покрыт четыре раза, но ни один из маленьких квадратиков выкинуть нельзя, — оголится соответствующая вершина. Квадратики можно заменить кругами радиуса чуть меньше единицы с теми же центрами. Прав sasha_br: пользовать ИИ для математических целей просто опасно. Он умеет какой-то морок насылать. Кто не видел, посмотрите на цитированный thread. (Read Comments |Comment on this)
lj_xaxam	5:35a	Duralex Блядство говорящих голов Чем характерно маленькое еврейское местечко — там по каждому вопросу есть максимум два эксперта (даже не обязательно раввины), обычно имеющие прямо противоположные мнения по данному вопросу. Поэтому якоря (anchors), ведущие разных аналитических и политических программ на радио/ТВ, изображая беспристрастность, на самом деле симулируют оргазм от давно порванной целки. Им прекрасно известно: кого пригласишь, того и услышишь. Конкретно. Недавняя "новость", — уголовника Биби™ суд с ноября месяца будет призывать к станку ответу 4 (четыре!) раза в неделю. Неча прохлаждаться в своём офисе, пусть чалится в присутствии. Если по-чеснаку, то Биби должен был бы перед судьяками на карачках ползать и пол лизать. На Лубянке, скажем, его бы допрашивала круглосуточная бригада следаков: один свою восьмичасовую вахту отстоял, рука бойца писать устала, — происходит смена караула. Приходит свеженький подвахтенный с новой чернильницей, а подозреваемый сидит как сидел. И так 24/7, благо в чекистах недостатка никогда не будет. Но у нас всё какая-то размазня сидит в курульном кресле. Жалкие четыре дня в неделю. Ну, и возмущённый говорящий голова поднимает в эфир™ эксперта-юриста, адвоката Пидоря Гнидера. Хорошо известного в узких кругах города Хуйфа. Эксперт оправдывает ожидания с первого слова: ну а как же! когда бибец баллотировался в Кнессет на последних выборах, юрсучка ему задала прямой вопрос, мол, как же ты, болезный, будешь одновременно справляться с двумя обязанностями, — защищать себя в суде против обвинения в краже бульона и десяти котлет и рулить страной, если победишь? И бибец поклялся мамой на коране, что ему никаких проблем не составит справиться с обеими миссиями. Что в общем не было бахвальством: конечно, допрос подозреваемого потребовал бы нескольких визитов в суд для дачи показаний, но в целом тяжесть обвинения выглядела настолько смехотворной, что бо́льшую часть времени в присутствии сидели бы адвокаты. Кто ж знал, что одни только показания свидетелей потребуют 4 года слушаний в суде: впервые бибец дал показания как обвиняемый только в декабре 2024 года! (дело подано в суд в 2020-м). Наивный читатель удивится: да что же такого изменилось между временем, когда бибец давал предвыборную клятву совмещать неприятное с бесполезным, и временем, когда был приказным характером объявлен график хождения в суд как на работу по три (а с ноября 2025 года и по четыре) дня в неделю? Никто не заметил? Ну вот и Пидорь Гнидер считает, что закон для всех один, суд состоится при любой погоде и порядок должен быть одинаков и для злостного неплательщика штрафов за парковку, и для премьер-министра воюющей на нескольких фронтах страны. Durex Dura lex, sed lex, суд надо уважать, велено ходить по четыре дня в неделю, — изволь ходить. Не можешь совместить такой режим с подработкой премьером по ночам и выходным — увольняйся с подработки... И ведь прав же Гнидер: нигде в законе не написано, что из-за войны премьер имеет право уходить в академический отпуск. Особенно учитывая, что у нас война перманентная: прими такой закон, — и ни один премьер никогда не пойдёт под суд. Но это в очередной раз возвращает меня к размышлению об устройстве общества. Общепризнанная идея сдержек и противовесов призвана мягко и без скрежета гасить противоположные даже не столько силы, сколько тенденции к развитию этих сил (идеальный пример — сопротивление в колебательном контуре). Однако усилиями наших медиа (только ли их?) эта система превратилась в собачьи бои. ❝Собачьи бои проводятся по специфическим правилам, которые зависят от породных клубов и традиций, но основные международные установки (например, UKC — Объединённый кеннел-клуб США) включают следующие элементы: Главные положения Бой обслуживается главным судьёй, назначенным обеими сторонами и имеющим разрешение соответствующей организации. Устанавливается хронометрист и обязательные процедуры взвешивания и регистрации собак. Собака считается проигравшей, если покинула свой угол без команды, проявляет пассивность или была поднята с арены без решения судьи. Организация и ход боя Бой проходит в специально оборудованной яме (обычно — квадрат 4,88 м со стенками). Перед боем собаки взвешиваются, купаются и обтираются при судье; проводится жеребьёвка по углам. После каждого раунда предоставляется короткий перерыв на обработку собак. Победа присуждается за доминирование, пассивность соперника или по техническим причинам. Поводы для дисквалификации Нарушение правил мытья, применение запрещённых средств, влияние на собак руками/предметами, вмешательство зрителей или организаторов. В некоторых традициях (например, японских боях тоса-ину) собака, скулящая или убегающая, немедленно проигрывает. Статус и законность Во многих странах собачьи бои запрещены законом как жестокое обращение с животными. Правила могут различаться в зависимости от региона, породы, организатора и уровня турнира; однако эти основы считаются наиболее распространёнными.❞  Каждая сторона норовит вывести самого зубастого и злобного бультерьера, чтобы выставить его на ринг в яму рвать на части противника. Что, в Израиле не нашлось судьи с большей склонностью к компромиссу, чем судьяк Амит? Что, религиозные сионисты не могут найти себе лучше полководца, чем тролль Бен Гвир? Что, иерусалимский судьяк, волокущий бибца вспоминать, какой рукой он разливал 10 лет назад бульон, в котором жарились котлеты, не понимает, что закон, конечно, превыше всего, но для воюющей страны есть более насущные вопросы, которые решать должен лично премьер? Но если Израиль в самом деле решил заменить сдержки и противовесы собачьими боями, то у меня есть рацпредложение. Надо набирать судей, прокуроров, армейских генералов, глав ШАБАКа и т.д. из числа завсегдатаев салона коллеги Иркудского (ну, или подобных же клубов интеллектуалов, чай он не один такой). Там анкетные данные всех участников выше любых мыслимых квалификационных требований: и средний IQ, и образовательный ценз, и социальное положение,— всё просто зашкаливает. А главное — хошь кого назначай председателем ревтрибунала, результат (задержание и противоповешенье) будет гарантирован. (Read Comments |Comment on this)
Friday, September 12th, 2025
lj_xaxam	6:55a	Злопамятность как социальное благо Математическая теория альтруизма — 2: даёшь движуху динамику Предыдущая сказка остановилась на интриге: можно ли придумать теоретико-игровую постановку, которая скрестила бы определённый здоровый эгоизм с социально выгодным альтруизмом к всеобщей выгоде. Предыдущая идея (фон Ноймана—Нэша), — рандомизировать задачу, заменив чистые стратегии смешанными и тем самым гарантировав существование решения, не помогает. Если в "Дилемме заключённого" мы имеем равновесие Нэша в чистых стратегиях, без рандомизации, то при рандомизации мы получим тривиально тот же ответ "с вероятностью единица". Ничего нового. Повторяющиеся игры Значит, искать надо в другом месте. В начале-середине 1980-х Роберт Аксельрод (вы можете полюбоваться на него в рекомендуемом видеоклипе) решил сменить Zeitgeist и рассмотреть "Дилемму заключённого" как повторяющуюся игру. Точнее, игра разыгрывается много раз, и ход каждого из игроков зависит от полной информации о том, как партнёр/противник (ПП) вёл себя в прошлом (разумеется, в предположении, что за поведением партнёра кроется некий алгоритм определения последующих шагов). Я Пастернака Аксельрода не читал (в своё время не имел доступа, а потом не имел уже того интереса), но основная суть его подхода не очень замысловата. Каждый из двух игроков имеет конечную память, и помнит последние m ходов (своих и ПП, партнёра/противника). На основе этих данных каждый игрок может попытаться предсказать, как сыграет в следующий раз, как нужно ответить самому, с пониманием, что ПП тоже запомнит такую реакцию. Что имеется в виду? Начнём со случая m = 0, оба игрока упёртые в стенку и знать не знают никакой предыстории. По понятной причине, ничего нового. Для простоты я буду кодировать ход каждого ПП одной из букв: "А" в честь альтруизма (молчать и не раскалываться) и "Э" в честь эгоизма. Игрок с нулевой памятью выберет один из вариантов, и будет долбить его до победного конца. Как только ПП поймёт, с кем имеет дело, он выберет вариант Э, поскольку никакой динамики в игре не будет. Всё то же унылое равновесие Нэша, которое нам очень не нравится. В случае, если m = 1, каждый из ПП должен решить, какой буквой, А или Э, ответить на предыдущий ход другого ПП. Вариантов реакции каждого из ПП всего четыре. На А ответить А. Благородно, есть надежда установить кооперацию: мы с тобой одной крови, ты и я. На Э ответить А. Вернись, я всё прощу, у нас есть шанс. На А ответить Э. Блядство, конечно, но в определённых условиях может быть оправдано. На Э ответить Э. Ну вот мы и вернулись к тому, с чего начали, не помогли нам никакие ляхи. Каждый может сам прикинуть, как будет развиваться дальнейшая динамика в предположении, что каждый из игроков вооружается одной из перечисленных четырёх стратегий. Вариант (1,1) — та самая entente cordiale, к которой все хотели бы устремиться. Вариант (4,4) — все в унылом говне, зачем только воду в ступе толкли. (1,2) или (2,1) — спросите у Чемберлена и Даладье, что может быть. Но самый убийственный вариант — 3. При внимательном рассмотрении он убивает все шансы на успех нахождения парето-оптимальной равновесной стратегии. Почему? Любая серия игр рано или поздно кончается. Предоложим, играть будут 200 раз (как в ролике), и это число известно обоим. Как будет выглядеть парето-оптимальная стратегия каждого из ПП на 200-м ходу? Очевидно. Бонусов от кооперации/альтруизма больше не будет, судьи заполняют протокол и тушат свет, а повторяющаяся игра автоматически превращается в одноразовую (последнюю в серии). Значит, каждый выберет Э. А что будет на 199-м ходу? Оба игрока знают, что в следующем ходу оба выберут Э, значит, никакого бонуса от кооперации на 199-м они не получат. Значит, будет (Э,Э). А на 198-м? рассуждая таким образом, мы доходим до первого шага, на котором выбор (Э,Э) становится оптимальным. Опять та же засада... Собственно, проблема возникает не только в теории игр, она известна и в обычной теории оптимизации под французским названием Après nous, le déluge. Пока надо как-то находить компромисс между потреблением и накоплением на будущее, надо соблюдать пропорции, но под конец эпохи инвестировать смысла не остаётся, поэтому можно всё пропить/проесть, после потопа никто этого уже не заметит. (Горделиво: в своей кандидатской я придумал, как можно ставить и решать подобные задачи, скажем, задачу динамического программирования, на бесконечном интервале времени, у которого нет верхней границы и проблемаЛуи XV исчезает). Аксельрод и Ко. по понятным причинам мои труды не читали, поэтому пошли по стандартному пути рандомизации: оба ПП знают, что их ждёт примерно 200 раундов на ринге, но когда точно прозвучит свисток, никому не известно. Я попробую объяснить ниже, как бы я решил проблему "финального свистка". Идея Аксельрода оказалась хоть и не очень замысловатой, зато очень богатой. Он объявил турнир. Все желающие присылали ему свой вариант "динамической стратегии", которая должна была бы найти компромисс между А и Э. Самая простая называлась tit-for-tat, глаз-за-глаз, имела память m = 1 и состояла в том, что ПП на следующем ходу отвечает так же, как другой ПП пошёл на предыдущем. На А ответить А, на Э ответить Э. Что произойдёт в долгой перспективе, если сойдутся два ПП, вооружённые этой стратегией? Всё зависит от первого хода, когда регистр памяти ещё пуст. Если оба ПП начинают с А, это самое А продержится до конца игры. Если оба начинают с Э, то это самое Э заклинится до конца. А что будет, если один скажет А, а второй Э в первом заходе? Результат описан в русской сказке "Лисица и журавль". Оба ПП будут по очереди сигналить А и Э, но в противофазе. Это принесёт результат заметно хуже, чем любая из стационарных "упёртых" стратегий: каждый ПП поочерёдно будет получать то червонец, то полную помиловку, в среднем — 5 лет за каждый раунд, много хуже, чем пара "нэшевских" стратегий (Э,Э), по двушечке без вариантов. Куда ни кинь, всюду клин. Или нет? Всё же нет. Во-первых, никто не обязывает ограничиваться памятью длины m = 1. Легко можно себе вообразить ситуацию, при которой каждый из ПП на каждом ходу принимает решения, глядя на m ≥ 2 последних ходов второго ПП. Во-вторых, можно попытаться понять стратегию второго ПП, глядя на то, какие ходы перед этим делал сам первый ПП. В-третьих, интересно посмотреть, как будут играть друг с другом два ПП с разными "стратегиями" самообучения и "дрессировки" второго ПП. В этом, собственно, и состоял турнир Аксельрода, — стравить между собой ПП с разными стратегиями и посмотреть, кто будет показывать лучшие результаты. Что такое стратегии? "История" длины m каждого игрока записывается m буквами, каждая из которорых либо А (альтруизм, молчать на допросе) либо Э (эгоизм, раскалываться и стучать). Всего возможных историй — 2m. Поскольку ПП-ов двое, — входная информация задаётся множеством из 2m+1 элементов, которое мы будем называть фазовым пространством Ф. Стратегия каждого из ПП — выбрать свою следующую букву, А или Э. Такой выбор представляется отображением фазового пространства Ф в себя, которое есть сдвиг на единицу по времени. При этом сдвиге самые первые (наиболее давние) буквы обеих историй забываются, остальные сдвигаются налево на одну букву, а на последнее место записываем новый ход, А или Э, свой для каждого ПП. Забывая к чёрту все подробности, мы видим, что пара ПП, каждый со своей стратегией выбора следующего хода, задаётся отображением ρ: Ф → Ф конечного множества Ф в себя (отображение отнюдь не абы какое — всё же "большая его часть" есть сдвиг на одну букву влево). Такая штука называется динамической системой, и её поведение однозначно определяется начальной точкой, т.е., парой m-историй, изначальных ходов игроков, которые непонятно откуда берутся. И что нам делать со всем этим хозяйством? Отображение ρ фактически задаёт нам сразу пару стратегий двух ПП. Осталось только понять, как оценить выгоду (выигрыш) каждого из ПП в такой "динамической игре". Для этого нам надо вернуться к исходной "Дилемме заключённого". В прошлой лекции мы говорили о конкретных сроках отсидки, которые прокурор назначает каждому из ПП в зависимости от его поведения. Традиционно вместо этого говорят о четырёх вещественных числах, традиционно обозначающихся буквами T,R,Р,S со следующими значениями: Если оба ПП молчат (выбирают букву А), то каждый получает вознаграждение R (reward); Если оба ПП стучат (выбирают букву Э), то каждый получает наказание P (punishment); Если один молчит, а другой стучит, то стукач получает выигрыш T (temptation), a упорный молчун получает "выигрыш" S ("sucker's payoff").   Для того, чтобы дилемма была нетривиальной, должны быть выполнены неравенства R > P (сотрудничество выгоднее эгоизма), а два других неравенства Т > R и P > S означают, что каждому по отдельности стучать выгоднее, чем молчать. Все эти неравенства вместе записываются одной цепочкой Т > R > P > S. Все эти выигрыши считаются положительными, поэтом сроки отсидки в исходной формулировке должны задаваться отрицательными числами 0 > −½ > −2 > − 10. Обычно добавляют ещё неравенство 2R > T + S, означающее, что "мигающая" пара стратегий "Лисица и журавль" нам не нравится и менее выгодна для каждого игрока, чем честное сотрудничество АА. Интегральная полезность всей серии повторяющихся игр определяется естественной формулой: к накопленной ранее сумме на каждом ходу каждому из ПП добавляют одну из четырёх величин T,R,P,S в зависимости от выбора каждого ПП, сделанного им на этом ходу. Это позволяет для любой конечной серии раундов и каждой "пары стратегий" ρ: Ф → Ф путём суммирования посчитать интегральную выгоду избранной пары стратегий для двух ПП, тем самым построив (ооочень непрямым образом) "динамическое расширение" исходной дилеммы заключённого, где вместо изначальных двух ПП соревнуются разные школы мастерства, предписывающие разные стратегии. Но задача формализации модели всё ещё не закончена. Непонятно, что делать, если: Число раундов бесконечно (иначе у нас будут-таки проблемы, см. выше): последовательности выигрышей на конечных отрезках могут легко расходиться как к плюс, так и к минус бесконечности; Неизвестны начальные условия итераций отображения ρ. Если стратегии участников имеют конечную глубину памяти m, то для вычисления реакции на следующем ходу надо иметь историю за последние m раундов. Откуда она возьмётся (особенно если m не очень мало, не раз-два — непонятно, чего предполагать).  В любом случае, анализ "метастратегий" — чертовски сложная задача.  Даже если мы упростим предположения, что каждый ПП смотрит исключительно на m-историю своего ПП и на основании этого принимает решения, — кооперироваться или "ну его нах", наказывая ПП выбором эгоистичного варианта, не сверяясь с тем, как он сам вёл себя на протяжении этой m-истории (и теми же соображениями руководствуется его ПП, но в рамках своей стратегии) — всё равно задача необозрима. Число индивидуальных историй длины m равно 2m, число возможных отображений этого множества в множество {А,Э} из двух возможных вариантов своей реакции — 22m, сиречь дохрена даже при не очень больших m. Перебрать все такие стратегии — и свести их в дуэли друг с другом (ещё в квадрат возведите) — мало не покажется ни одному аспиранту, программирующему на бейсике/коболе. Что делать Как считать? (Азы теории динамических систем) Вернёмся к абстрактной ситуации, отображения ρ: Ф → Ф конечного множества в себя. Оказывается, конечность Ф позволяет сделать очень важные выводы. Напомним, что орбитой (или траекторией) точки x ∈ Ф под действием отображения ρ называется бесконечная последовательность точек x, ρ(x), ρ2(x) = ρ(ρ(x)), ρ3(x) = ρ(ρ(ρ(x))), ... Орбита называется стационарной, если ρ(x) = x, т.е., если она состоит из единственной точки. Обобщением стационарной орбиты является периодическая орбита, такая, что ρp(x) = x для некоторого p ≥ 2; минимальное значение такого p называется периодом. Периодическую орбиту называют также циклом. Теорема. Любая орбита из конечного множества начиная с какого-то момента становится периодической (или стационарной). В самом деле, из-за конечности Ф любая (бесконечная) орбита обязана в какой-то момент t "наступить себе на хвост", т.е., для каких-то двух разных моментов t < s случится равенство ρt(x) = ρs(x). Но это означает (почему?), что точка ρt(x) будет периодической с периодом p = s − t. Начиная с этого момента, орбита будет бесконечно крутиться по циклу с периодом p (мы будем говорить, что орбита "намоталась" на цикл. Разные орбиты, конечно, могут наматываться на разные циклы, но общее число разных циклов тоже конечно по очевидной причине: разные циклы не пересекаются друг с другом (почему?). Отсюда следует, что любая орбита на конечном множестве Ф за конечное число шагов намотается на один из непересекающихся циклов с суммой периодов не больше | Ф | (числа элементов в Ф). Что из этого элементарного наблюдения следует для нашей итерированной дилеммы заключённого? Напомним, что Ф в данном случае — конечное множество всех "историй" длиной ≤ m, так что | Ф | = 2m+1, а ρ — отображение "следующий ход" (сдвиг на единицу влево с добавлением новой пары из двух букв А и Э). В результате хода каждый из игроков (ПП, партнёр/противник) увеличивает свой накопленный (интегральный) выигрыш на одно из четырёх чисел T, R, P, S в зависимости от сделанного хода. Можно ли приписать конечный выигрыш бесконечной траектории? Ответ утвердительный, если траектория периодическая с конечным периодом р. В самом деле, тогда выигрыш, накопленный за период каждым игроком, будет конечным (не больше, чем Т⋅р и не меньше, чем S⋅р), и за каждый период будет накапливаться одно и то же число. Если сравнивать средний выигрыш за один шаг, то мы получим для каждого игрока после деления на р своё число, описывающее выигрыш "на бесконечной траектории". Наличие конечного непериодического отрезка траектории при усреднении на общее число шагов не меняет предельного среднего значения. Иными словами, выигрыши двух ПП в бесконечной серии раундов могут быть легко сравнены между собой, избавляя нас от необходимости искусственно вводить ограничение на длину серии, и эти выигрыши имеют смысл интегрального суммарного выигрыша за t раундов после деления его на t в пределе, когда t растёт до бесконечности. Фактически, выше приведено объяснение, как считать этот предел за конечное число арифметических/графовых операций. Что считать? Напомним основной содержательный вопрос, с которого начался весь длинный разговор. Есть два игрока (ПП), у каждого из которых есть в каждый момент выбор между альтруистическим выбором А и эгоистическим выбором Э. Если игра проводится в один раунд, то оба ПП имеют все основания выбрать Э, но этот выбор неоптимальный: оба ПП выиграют больше, если скоординируют усилия и оба выберут А. Можно ли "принудить" игроков выбирать альтруистическую стратегию, если заставить их играть достаточно долго? Интуитивно ясно, что игроки должны "обмениваться сигналами", пользуясь дипломатическим языком. Выбирая А, каждый игрок сигнализирует "добрую волю", готовность к кооперации. Выбирая Э, игрок "наказывает" ПП за плохое поведение, проявленный эгоизм. Правила, определяющие, когда ходить А, а когда Э в зависимости от предыдущих ходов, будем называть стратегией каждого игрока. Предположим наиболее простой случай: Стратегия каждого игрока определяется только предыдущими m ходами его ПП (и не зависит от его собственных m предыдущих ходов, — "а меня-то за что наказывать?"). Это на самом деле означает "искать под фонарём", но надо же начинать с чего-то более простого. Тем самым мы имеем фазовое пространство Ф в виде слов длиной m из двух букв А и Э (что каждый игрок помнит про поведение ПП), | Ф | = 2m. Стратегия каждого игрока — сопоставить такому слову x одну из "своих" букв А или Э. Общее число возможных стратегий — 22m. Даже если предположить, что память у игроков девичья, m ≤ 5, число 232, это больше миллиарда. Свести на ринге весь этот миллиард друг с другом нереально. Значит, надо ограничиться стратегиями по возможности более примитивными. Сформулированный выше "интуитивный" принцип подсказывает, что реакция каждого игрока на поведение ПП должна поощрять проявленное кооперативное поведение, сделав ход А, и наказывать проявленный эгоизм, сделав ход Э. Пороговые стратегии. Самое первое, что приходит в голову, — каждый из игроков выбирает для себя "пороговую толерантность", вещественный параметр μ ∈ [0,1], и смотреть на слово х, описывающее послужной список ПП: если доля букв А в нём больше, чем μ — надо поощрять ПП и ходить тоже А. А если доля букв А меньше порога μ — надо наказывать ПП, ходя Э. Чем больше μ, тем стратегия более "сердитая", чем этот порог ниже, тем стратегия "мягче, доверчивей". Если бы аксельродом был я, я бы написал соответствующий скрипт и посмотрел, при каком значении μ "сердитая" стратегия перестаёт быть более выгодной, чем "доверчивая". Я на сто процентов уверен, что ответ (экспериментальный) должен зависеть от платежей T,R,P,S. Что делать Сам Аксельрод организовал турнир между разными стратегиями, далеко не столь простыми, как предлагаемые "пороговые". Например, одна из стратегий предписывала наказывать ПП не за однократное проявление эгоизма, а за две подряд буквы Э, сыгранные против двукратного предложения А. В результате он пришёл к следующему описанию того, как должна выглядеть "правильная стратегия", принуждающая ПП к кооперации (чаще ходить А, чем Э). Стратегия должна быть доброй (nice), т.е. никогда не проявлять беспричинный эгоизм, и не ходить Э в то время как ПП ходит А. Стратегия должна быть достаточно мстительной (retaliate) чтобы не позволить ПП злоупотреблять твоей добротой. Стратегия должна уметь прощать (forgiving), чтобы дать возможность ПП исправить какие-то случайные ошибки. Стратегия должна быть не завистливой (non-envious), т.е. не пытаться непременно набрать больше, чем противник. Выглядит как призыв бороться "за всё хорошее против всего плохого". Первое свойство, конечно, не вызывает сомнений, если целью будет найти стратегию, которая приводила бы к парето-оптимальности на бесконечном промежутке времени. Но уже найти правильный баланс между мстительностью и готовностью прощать — проблема, которую надо решать на основании точных подсчётов. Именно попытка найти компромисс между этими двумя принципами и побудила меня предложить класс пороговых стратегий, описанный выше. Пороговых стратегий (при каждой фиксированной глубине памяти) совсем не так много, их можно стравливать друг с другом и смотреть на результаты, кто получит большую выгоду в среднем на один ход. Ну и вот ещё раз ссылка на видос, с которого всё началось: Энжуйте на здоровье! (Read Comments |Comment on this)
syn_trv_science	12:46a	Над пропастью — о жизни Книжная полка «Троицкого варианта» пополнилась еще одним изданием. «Место жизни во Вселенной» — расширенный и переработанный сборник интервью для ТрВ-Наука, посвященный жизни: тому, когда и как она возникла на нашей планете, как эволюционировала, как появился фотосинтез, многоклеточные животные и мы, разумные мыслящие существа; можем ли мы встретить эту жизнь где-то еще, в далеких звездных системах; и каковы шансы распространить ее на пока еще необитаемые планеты с подходящими природными условиями. Авторский коллектив хорошо знаком нашим читателям: это Михаил Гельфанд, Евгений Кунин, Александр Марков, Армен Мулкиджанян, Михаил Никитин, интервью же с ними проводил главный редактор ТрВ-Наука Борис Штерн. Сообщение Над пропастью — о жизни появились сначала на Троицкий вариант — Наука. (Comment on this)
Thursday, September 11th, 2025
tiphareth	11:15p	Sydney Sweeney Has Great Bath Water Смешное AI-видео https://www.youtube.com/watch?v=Grw6ytFdGkk Sydney Sweeney Has Great Bath Water про акивистов демократической партии (Байдена, Обаму, и Клинтона с женой, с накладными усами и в бейсболке Make America Great Again) которые пытаются украсть у красивой голой Сидни Свини воду из ванной, а Трамп их ловит и предает правосудию. Все это под музыку, тоже прямо из Суно. Скоро вообще никаких видео не будет, только AI, и не надо нахуй Привет Current Mood: sick Current Music: Sydney Sweeney Has Great Bath Water (119 Comments |Comment on this)
syn_trv_science	8:33p	ТрВ № 18 (437) за 2025 г.: Над пропастью — о жизни Твердое ядро Марса, молодые звезды в М96… Семь летних дней в НИИЧАВО. Гейзенберг, Борн, Паули — кто больший осёл? От партизана до математика. Зрение людей, животных и машин. Перевод с вещи на вещь. Опасный совет героя коллоквиума. Психология и только психология. Милосердие и человечность. Кто не хочет быть Машенькой. ТрВ-Наука № 437 от 9 сентября 2025 года в PDF Материалы номера в HTML Сообщение ТрВ № 18 (437) за 2025 г.: Над пропастью — о жизни появились сначала на Троицкий вариант — Наука. (Comment on this)
lj_xaxam	6:46a	Об эгоизме без политики Что такое альтруизм с точки зрения математики Почтеннейший lazybiker мне прислал ссылку на замечательный видеоклип, посвящённый тому, что с эволюционной точки зрения выгоднее, эгоизм или альтруизм. Теоретически каждый сам может посмотреть этот клип (он на русском), не читая нижеприведённый текст. Но мне кажется, что этот текст может послужить полезным предисловием для тех, кто никогда не сталкивался вообще с теорией игр и принятия решений. По техническим причинам он будет разбит на несколько постов. Теория игр: почём за вист? Давайте поговорим о том, что есть вся наша жизнь — игра. Понятие игры выросло из понятия максимизации (ну, или минимизации), которую человечеству приходилось решать со времён царя Гороха. Есть несколько вариантов, каждый из которых имеет свою цену (ну, или наоборот, выгоду, полезность), надо выбрать наилучший вариант. Если вариант всего один, то задачи нет. Выбор из двух вариантов учатся делать младенцы, а из конечного (небольшого) числа — младшеклассники, которых учат сравнивать числа. Сложность возникает тогда, когда вариантов слишком много, чтобы их перебирать. Например, классическая "задача Дидоны" (она же изопериметрическая задача) — имея замкнутую верёвку длиной 100 метров, выложить её на землю так, чтобы огородить наибольшую площадь. Другая задача (описывающая преломление света) — скорейший путь. Есть пустошь и вспаханное поле, граница между которыми — прямая линия. Человек идёт по пустоши быстрее, чем по полю (скорости известны). Вбиваем два колышка: один на пустоши, другой на поле. Как проложить самый быстрый путь между колышками? Хорошо если колышки вбиты на одном перпендикуляре к границе между пустошью и полем: иди по прямой, и уж сколько понадобится, столько и потратишь времени, меньше никак не получится (почему?). А если нет? Если прямая линия между колышками пересекает границу под острым углом? Очевидный ответ: надо наметить себе точку на границе, и идти вдоль прямых отрезков, соединяющих эту точку с двумя колышками. Но где выбрать эту точку? Все сказанные задачи сводятся к поиску минимума/максимума функции одной переменной, таким задачам учат первокурсников. Богатство выбора может быть ещё больше. Представим себе "водную горку", по которой дети с определённой высоты скатываются и плюхаются в бассейн с водой. Стартовая и финишная точки фиксированы, но собственно форма горки — в нашем распоряжении. Как выбрать эту форму так, чтобы ребёнок скатывался за кратчайшее время? (Задача была поставлена в 1696 году и решена независимо всей плеядой тогдашних великих математиков — братьями Бернулли, Лопиталем, Ньютоном и Лейбницем). С математической точки зрения задача сводится к минимизации "функции бесконечного числа переменных", т.н. вариационной задаче, решению которых учат уже на старших курсах. Но идейно все такие задачи различаются только техникой максимизации. Игры — принципиально иной класс задач. В теории игр есть не одна-единственная функция, которую нужно максимизировать, а несколько разных функций, по числу игроков. Если каждая функция задана на своей области определения и они никак не связаны между собой, то игроки не обращают друг на друга внимания и каждый решает свою задачу оптимизации. Движуха возникает, когда функции определены на общей области определения. В простейшей ситуации, когда у нас два игрока и минимальная область определения, возникает следующая задача. Пусть первый игрок "управляет" переменной икс, принимающей значения, скажем, на отрезке [a,b], а второй управляет игреком, который можно выбрать из отрезка [c,d]. Первый игрок хочет максимизировать некую функцию f, второй — свою функцию g. Если бы f зависела только от x, a g — только от y, мы бы имели две не связанные оптимизационные задачи. Но мы хотим исследовать именно движуху, когда обе функции зависит каждая от обеих переменных, f = f(x,y), g = g(x,y). Обе функции известны обоим игрокам, но свой выбор (икс и игрек) они делают независимо и одновременно друг от друга. Почему это важно? Предположим, что функция g на самом деле не зависит от икса. Тогда стратегия второго игрока очевидна: он максимизирует свою функцию g, выбирая нужный игрек, y0. Зная это, первый игрок будет рассматривать функцию только одной переменной, f(x,y0), и выберет значение икса, дающего максимум. Никакой интриги нет. Альтернативная игра (кажется, простейшая возможная) — каждый из двух игроков кладёт на стол монету, орлом или решкой вверх. Первый игрок получает рубль, если две монеты легли одинакого, и ничего не получает, а второй получает рубль, если монеты легли разными сторонами (и ничего, если одинаково). В этой ситуации если один из игроков положит свою монету на долю секунды раньше — он не получит ничего, а второй получит свой рупь. Никакой "оптимизации" и близко не просматривается. Чуть более сложный вариант той же игры — "камень, ножницы, бумага". В обоих случаях каждый из игроков выбирает один из двух (или трёх) возможных ходов, так что никаких технических проблем с нахождением максимумов нет, есть исключительно концептуальные. Можно ли хоть в каких-то ситуациях предсказать "оптимальное поведение" игроков? Один тривиальный случай мы уже разобрали, не найдя в нём ничего интересного. Оказывается, можно найти чуть менее тривиальный, но всё ещё полностью обозримый случай. Это так называемые игры с седловой точкой. Определение. Седловой точкой игры называется такая (допустимая, разумеется) пара, "совместный" выбор двух игроков (x0, y0), который ни один из игроков не хочет менять ни на что другое. Это значит, что выгода первого игрока f(x,y0), рассматриваемая как функция одной переменной ("своей", икса) достигает максимума "как раз" в точке x0, и одновременно с этим выгода второго игрока g(x0, y) как функция "своего" игрека тоже достигает максимума "как раз" в точке y0. Такая седловая точка приносит одновременный максимум обоим игрокам. При одном условии: если она существует. Каждый из игроков, зная функции выгоды (свою и противника) может (в случае конечного числа возможных ходов) перебрать все возможные пары исходов, и если среди них найдётся седловая точка, то каждый из игроков выберет именно её за неимением лучшего варианта. Но вот беда. Даже самая простая игра "в две монетки" не имеет седловой точки! В самом деле, все многообразие возможных ходов сводится к четырём: (О,О),(О,Р), (Р,О) и (Р,Р). Проверьте, что (одномерная) максимизация выгоды, скажем, первого игрока зависит от выбора второго (и наоборот), поэтому универсального выигрышного варианта тут нет (это, впрочем, и так очевидно). Что же делать? Ответ угадал один из самых гениальных и разносторонних математиков 20 века, Джон (Янош, Янчи) фон Нойман сто лет назад, в 1928-м году. Он придумал понятие смешанной стратегии, расширения игры, включающего генератор случайных чисел. Пафос в том, что показания датчика случайных чисел неизвестны никому, включая того игрока, который им пользуется. Стратегия состоит в настройке датчика. Проще всего объяснить понятие смешанной стратегии в случае, когда множество допустимых ходов каждого игрока — конечное множество вариантов x1, x2, ... , xn и y1, y2, ... ym соответственно. Определение. Смешанная стратегия игрока, контролирующего иксы, есть распределение вероятностей на пространстве ходов, приписывающее ходу xi неотрицательную вероятность pi, i = 1, ..., n, так, чтобы сумма вероятностей была единичной. Соответствующей смешанной стратегии xp приписывается "расширенная функция выгоды" f(xp,y) = ∑ pi f(xi,y) (обычное математическое ожидание, никаких сюрпризов). Аналогично определяются смешанные стратегии второго игрока. Какое радикальное изменение с точки зрения математики произошло при рандомальном расширении игры, допускающем смешанные стратегии? Гигантское. В исходной постановке пространства допустимых ходов были конечными множествами без всякой дополнительной структуры. Функции выгоды каждого из игроков задавались таблицами ("платёжными матрицами"), тоже априори не несущими никакой структуры. С введением смешанных стратегий мы фактически заменяем дискретное конечное пространство допустимых ходов геометрической фигурой, называемой симплексом: множеством точек в ℝⁿ с неотрицательными координатами, в сумме дающими единицу. Это — топологическое пространство, "непрерывное" (без разрывов, дыр и скачков), и рандомально расширенная функция выгоды будет автоматически непрерывна по всем переменным. Это обстоятельство, в свою очередь, позволяет "интерполировать" конкретные допустимые ходы, заменяя их "лотереей", исход розыгрыша которой неизвестен никому, пока ход не сделан. Фон Нойман доказал (очень несложными рассуждениями), что в одном, но практически очень важном классе игр с нулевой суммой (когда выигрыш одного игрока равен проигрышу другого, т.е., цели игры абсолютно антагонистичны) рандомально расширенная игра, допускающая смешанные стратегии, всегда имеет седловую точку. Иными словами, каждый игрок имеет выигрышную беспроигрышную стратегию. В случае игры в две монетки достаточно бросать свою монетку случайным образом. (Технически эта игра с ненулевой суммой, но её можно свести к чисто антагонистической, когда при совпадении второй платит первому полтинник, и наоборот, получает от первого полтинник, когда монетки легли разными сторонами). Следующий ключевой шаг в теории игр сделал гениальный безумец Джон Форбс Нэш, получивший нобелевку по экономике за свою кандидатскую (Ph.D.) диссертацию. Он обобщил понятие седловой точки в игре двух игроков с нулевой суммой до понятия "равновесия по Нэшу". Глобально идея та же самая: есть несколько игроков, каждый выбирает из конечного множества доступных ему ходов, все игроки вместе определяют "коллективный ход". Такой ход называется "равновесным по Нэшу", если ни один игрок не имеет причины сменить свой выбор (увеличив свою личную выгоду) при условии, что остальные его не поменяют. Теорема Нэша утверждает, что равновесие по Нэшу всегда существует в классе смешанных стратегий (т.е., при описанной выше рандомизации игры). В отличие от конструктивного доказательства фон Ноймана, доказательство Нэша опирается на самые общие топологические теоремы анализа (типа теорем о невозможности причесать круглого ежа). Что мы имеем с игривого гуся? Парето-оптимальность Мы имеем попытку определить, что такое "решение игры", т.е., аналог понятия мульти-максимума, одновременного максимума нескольких функций, описывающих выгоду. Такие попытки предпринимались сотни лет назад. В частности, Вильфредо Парето (сто лет назад) явно сформулировал концепцию, которая была очевидна всем на свете. Что такое "максимум векторнозначной функции"? Например, каждой точке из допустимого множества вариантов сопоставим точку на плоскости "оценок" ℝ² с координатами x,y. Как определить одновременный максимум обеих координат на множестве М допустимых вариантов? Проще объяснить, что не является максимумом. Допустимая точка (x0,y0) не является одновременным максимумом, если существует другая допустимая точка (x1,y1) такая что x0  ≤  x1 и y0 ≤ y1, причём хотя бы одно из неравенств является строгим. Мы будем называть такое отношение порядка "слабым улучшением" за неимением лучшего слова ("кому-то приятно, а остальным всё равно", как в анекдоте). Если мы выбросим все точки, которые остаются, то мы получим "северо-восточную границу" множества М на плоскости. Такие точки на границе называются оптимальными по Парето (или парето-оптимальными). Плюс такого понятия — парето-оптимум существует в разумных технических предположениях (например, когда множество М компактно). Минус, — таких оптимумов обычно слишком много, если мы хотим определённости, то надо как-то сравнивать между собой независимые критерии оценки x, y. Но главное, "ключевое" свойство парето-оптимальности — любое "разумное" определение решения игры должно быть парето-оптимальным, т.е., не допускать слабого улучшения. В самом деле, если есть две пары ходов, (x0,y0) и (x1,y1) (ахтунг: икс и игрек теперь обозначают допустимые ходы двух игроков), и при этом f(x0,y0) ≤ f(x1,y1) и g(x0,y0) ≤ g(x1,y1), где f, g — функции выгоды этих игроков и хотя бы одно из неравенств является строгим, то оба участника заинтересованы в том, чтобы променять (x0,y0) на (x1,y1): это будет слабым улучшением, ни один из них от такой смены не проиграет, а один даже выиграет (мы считаем, что "злорадство" не является фактором в игре, каждый смотрит только на свою выгоду). Понятие парето-оптимальности кажется совпадающим с понятием равновесия. И равновесие по Нэшу, и парето-оптимальность состояния (x0,y0) "неформально" означают, что ни один игрок не может улучшить своё состояние, избрав альтернативный вариант своего хода. Но как всегда, тонкости в деталях. Равновесие по Нэшу означает, что ни один из игроков не может в одиночку увеличить свой выигрыш при условии, что второй игрок сохраняет свой выбор (если игроков больше двух, то в предположении, что свой выбор сохраняют все остальные игроки). Напротив, парето-оптимальность подразумевает, что, даже действуя вскладчину (кооперируясь, согласовывая свои ходы), игроки не смогут слабо улучшить свои результаты. 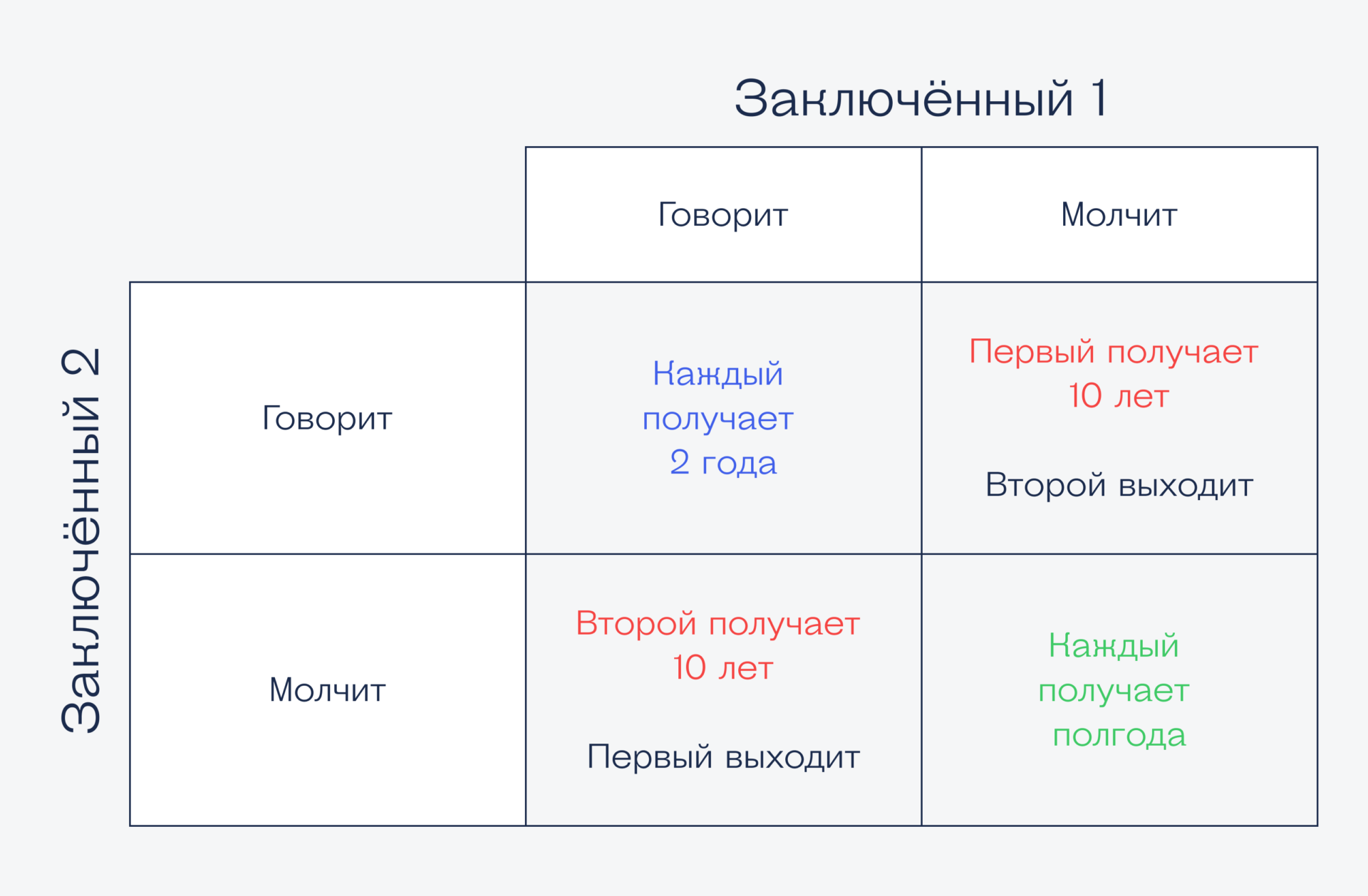Дилемма заключённого Из приведённого описания следует, что парето-оптимальное решение будет равновесием по Нэшу: если его нельзя слабо улучшить коллективными усилиями, значит, усилиями каждого игрока его и подавно нельзя слабо улучшить. Но может быть, по каким-то причинам, по крайней мере для не слишком сложных игр верно и обратное, и равновесие по Нэшу будет парето-оптимальным? Увы, всего спустя всего 6 лет после выхода эпохальной монографии фон Ноймана и Моргенштерна "Теория игр и экономическое поведение" в 1944 году, двое сотрудников RAND Corporation описали игру (не антагонистическую), когда равновесие по Нэшу не является парето-оптимальным. В привычном виде под названием "Дилемма заключённого" её сформулировал Альберт Таккер. Если вдруг кто-то случайно не слышал про этот шедевральный пример, вот в чём состоит игра. Прокурор посадил в КПЗ двух подозреваемых в совершении преступления, они сидят в разных камерах и не могут общаться между собой. Прокурор пытается "расколоть" их, каждого по отдельности, признаться в совершении преступления. У каждого из двух есть две опции: говорить или молчать. Прокурор сочетает кнут и пряник и говорит каждому из подозреваемых: если вы оба сознаетесь, я дам вам по "двушечке", просто чтоб не оставлять преступление безнаказанным. Если один из вас сознается, а второй будет молчать — сознавшийся получает прощение за сотрудничество с прокуратурой, а упрямцу я вкачу червонец. Наконец, если вы оба будете молчать — я посажу вас обоих на полгода каждого за нарушение общественного порядка. В этой игре, как и следовало ожидать, есть равновесие по Нэшу, и даже в чистых (а не в смешанных, рандомизированных) стратегиях. Но оно "парадоксально": обоим подозреваемым есть смысл расколоться и признаться. Почему? Рассмотрим первого игрока. Если он выбирает "говорить", то в зависимости от того, что сделает второй, первый получит либо двушечку, либо вообще помиловку. Если же он будет упираться, то получит либо червонец (вместо двушечки), либо полгода (вместо помиловки). В обоих случаях первому выгодно расколоться. Поскольку ситуация симметрична, те же аргументы справедливы и в отношении второго игрока. Итак, вариант "расколоться" выгоден обоим с точки зрения равновесия Нэша, и оба присядут на двушечку. Но это же глупость: если б они смогли скооперироваться и оба отпирались бы, то каждый получил бы по полгода, что как ни крути лучше двушечки. Тем самым равновесие по Нэшу не парето-оптимально. Вопрос можно переформулировать в несколько иной форме. У игроков есть кооперативная "альтруистская" стратегия (оба молчат), и при этом у каждого есть "эгоистическая" стратегия обеспечить себе лучший из вариантов при любом действии партнёра. Парадокс заключённого обычно интерпретируется как дилемма между альтруизмом и эгоизмом: альтруизм выгоден "коллективу" (обоим игрокам), а эгоизм - каждому по отдельности. Положение скверное. Мы (ну, не мы, а Нэш, конечно) придумали понятие решения игры, которое прекрасно тем, что всегда существует. Но беда в том, что оно "плохое", а мы за всё хорошее, в частности, за то, чтобы лучше было всем. Можно ли что-нибудь сделать в такой ситуации? Чтобы сделать альтруистический выбор, надо иметь "доверие к партнёру", какую-то уверенность, что он будет руководствоваться общей выгодой, а не своей личной. Но понятие доверия не входит в лексикон теории игр, значит, его надо чем-то заменить. Но чем? Ответ — послужным списком. А как именно — я расскажу в следующий раз. (Read Comments |Comment on this)

[ << Previous 25 -- Next 25 >> ]