|
|
| Пишет ivanov_petrov ( @ 2012-01-29 13:21:00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Клетчатый вызов
Вызывающее утверждение http://xaxam.livejournal.com/456151.html
sgustchalost: Углы 90 град трудно делать.
Всяческие автоволны химической или информационной природы обычно полосатые или пятнистые.
http://xaxam.livejournal.com/456151.html?t
и далее спор
- Странный аргумент. Если взять прямоугольную пластинку, то среди "собственных мод" вполне будут формы f(x).g(y) с квадратной решёткой.
И угол делать очень просто: согнул пополам, и ещё раз пополам ;-)
- Ну спорить не полезно и не буду.
Чтобы взять прямоугольную пластинку, её надо сначала сделать. А природа этого не умеет.
В исск. условиях вполне можно вырастить и кубическую голову, и хамелеона в клеточку поиметь.
Опять же формы из бесформенности в природе возникают не в твердо-кристаллической, а в "вязкой и диффундирующей" среде, где решетчатые моды трудно мыслимы. Если обнаружите - смело посылайте в J Theor Biol, неплохой журнал.
- В вязкой и диффундирующей среде возникают, скажем, ячейки конвекции Рэлея-Бенара, которые "плотно заполняют" доступное пространство и поэтому оказываются расположенными в гексагональной решётке.
Возникновение паттернов на шкурах животных - одна из самых прелестных тем теоретической биологии: они, с одной стороны, так же уникальны, как отпечатки пальцев, с другой стороны, глядя на зебру, нет сомнения, что это зебра а не гепард или тигр.
В основном эти процессы моделируются уравнениями типа "реакция-диффузия", и там, действительно, чаще всего возникают волны ("полосы"), иногда спиральные волны (редко, но попадаются). С другой стороны, я не знаю никаких причин, почему бы решениям таких уравнений не иметь двоякопериодическую симметрию (пускай параллелограммы, а не квадраты). Лапласиан ведь инвариантен ко всем вообще движениям плоскости...
О чём, в сущности, и был вопрос.
- Ну, мы поняли друг друга.
1. Как вы и сказали рядом, гексагон - распространеннейшая вещь.
2. Ага.
3. Кстати, параллелограммы вроде бывают. Не на шкуре, а в тканях растений. Там еще механика включается.
ПРЯМОУГОЛЬНИКИ - нет.
4. Возможно, ответ и содержится в книге В.В.Смолянинова "Математические модели биологических тканей, которую я до утра "корректировал" перед госами. Но её прочитало пять человек, а поняло ноль (если Гельфанд не читал, а он вроде из вредности не читал.) Сейчас она еще и труднодоступна.
ЗЫ. Как уже было сказано, будет модель квадратов в уравнениях типа "реакция-диффузия", будет вам и хирш с маслом и икрой.
--------------------
В пример приводят черепах и соты пчел. Но их выводят под руку из зала: це гексагоны, сплющенные круги, а не квадраты.
Я вспомнил работу Креславского, специалиста по листоедам. У него был большой текст по закономерностям окраски жуков. Там говорилось, что странным образом в Евразии листоеды обычно полосаты (если не гладкая окраска, а северной Америке они чаще клетчатые, и можно видеть некоторые области интерградации, где клетчатые наползают на полосатых и наоборот.
Я полез посмотреть, что за листоеды в Америке

Cerotoma trifurcata

Aulacophora hilaris



Gonioctena fornicata

наскоро чего-то насобирал. Кажется, эти примеры тоже отведут - мол, просто пятнистые. Помню, бывают тесно расположенные пятна именно что крадратные, но эта квадратность не выдерживается на всем надкрылье - все же становятся они к углам, эти квадраты, многоульниками и овалами.
Отдельные квадраты найти можно, хотя бы у Cleridae, Buprestidae и в других семействах, у чернотеклок, усачей, бронзовок и пр.




Castiarina sexplagiata

Coccinella transversoguttata

Neonectes natrix
Но вот прямо четких квадратов нет. Как я понимаю, да, делать регулярно прямые углы трудно, расплываются. Жидкие системы, что тут сказать.
То есть при описании системы окрасок зоолог может сказать, что у каких-то форм квадраты в отличие от полос. Но это именно утверждение о типе окраски, а не о точной геометрии - если к этому прикладывать строгие критерии и действительно измерять углы и прямые, так не будет точных квадратов.
Однако можно, если подумать, переформулировать немного задачу. Нас волнует не точность углов квадрата, а сам тип стрктуры - клетчатый, пусть даже с некоторыми искажениями. тут важны не параметры отдельной ячейки, а паттерн их совокупности. Окраска - не очень удобный пример, все-таки цвет в геле образхуется, выделяясь из б.м. локального центра, потому границы округлые и нечеткие. Но есть и другие задачи.
Это могли бы быть ребра жесткости. В натянутой пленке ребра жесткости могут создавать решетчатую структуру.
Паутина так сделана. Общая ее форма ее округлая, но эта окружность разеделена на ячейки, на внешних границах они напоминают прямоугольные.
Но это все же отговорка - сама паутина обычно все же округлая. значит, нам нужна паутина как орган тела, входящая в состав общей пластинчатой формы.
Это будет архедиктион, крыло древних насекомых.

Подобные крылья у стрекоз и поденок.
Там видна эта самая сетка ячеек


Наконец, жалко не найти этого у жуков, раз уж начал искать.
У жуков передние крылья стали надкрыльями, а древняя сеть жилок стала рядами каннелюр, такой желобчатой решетчатой структурой.
Я сейчас не соображ кого имеет смысл искать в рисунках гугля, так-то этого дела полно. Самый легко приходящий в голову пример у Archostemata, Cupedidae

У этих жуков четко видны квадратные и прямоугольные решетки на диске надкрыльев.
Это вот так может выглядеть
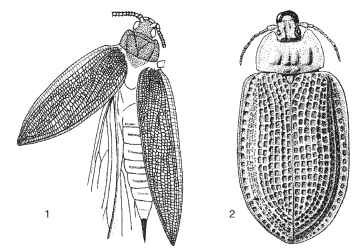
Notocupes picturatus (Cupedidae: Coleoptera, Triassic)
Если угодно, можно сказать, что решетки водились на земле в прошлые времена и в основном вымерли
Ну что же. Вот чешуйки на крыльях бабочек


хотя могут быть и такими

Итак, звери оправданы - могут.
Вызывающее утверждение http://xaxam.livejournal.com/456151.html
никто ещё никогда не видел ни одного живого существа в клеточку
Узоры в клеточку - главное интеллектуальное достижение человечества, вознесшее его над животными и проложившее путь к декартовой системе координат и римановой геометрии.
sgustchalost: Углы 90 град трудно делать.
Всяческие автоволны химической или информационной природы обычно полосатые или пятнистые.
http://xaxam.livejournal.com/456151.html?t
и далее спор
- Странный аргумент. Если взять прямоугольную пластинку, то среди "собственных мод" вполне будут формы f(x).g(y) с квадратной решёткой.
И угол делать очень просто: согнул пополам, и ещё раз пополам ;-)
- Ну спорить не полезно и не буду.
Чтобы взять прямоугольную пластинку, её надо сначала сделать. А природа этого не умеет.
В исск. условиях вполне можно вырастить и кубическую голову, и хамелеона в клеточку поиметь.
Опять же формы из бесформенности в природе возникают не в твердо-кристаллической, а в "вязкой и диффундирующей" среде, где решетчатые моды трудно мыслимы. Если обнаружите - смело посылайте в J Theor Biol, неплохой журнал.
- В вязкой и диффундирующей среде возникают, скажем, ячейки конвекции Рэлея-Бенара, которые "плотно заполняют" доступное пространство и поэтому оказываются расположенными в гексагональной решётке.
Возникновение паттернов на шкурах животных - одна из самых прелестных тем теоретической биологии: они, с одной стороны, так же уникальны, как отпечатки пальцев, с другой стороны, глядя на зебру, нет сомнения, что это зебра а не гепард или тигр.
В основном эти процессы моделируются уравнениями типа "реакция-диффузия", и там, действительно, чаще всего возникают волны ("полосы"), иногда спиральные волны (редко, но попадаются). С другой стороны, я не знаю никаких причин, почему бы решениям таких уравнений не иметь двоякопериодическую симметрию (пускай параллелограммы, а не квадраты). Лапласиан ведь инвариантен ко всем вообще движениям плоскости...
О чём, в сущности, и был вопрос.
- Ну, мы поняли друг друга.
1. Как вы и сказали рядом, гексагон - распространеннейшая вещь.
2. Ага.
3. Кстати, параллелограммы вроде бывают. Не на шкуре, а в тканях растений. Там еще механика включается.
ПРЯМОУГОЛЬНИКИ - нет.
4. Возможно, ответ и содержится в книге В.В.Смолянинова "Математические модели биологических тканей, которую я до утра "корректировал" перед госами. Но её прочитало пять человек, а поняло ноль (если Гельфанд не читал, а он вроде из вредности не читал.) Сейчас она еще и труднодоступна.
ЗЫ. Как уже было сказано, будет модель квадратов в уравнениях типа "реакция-диффузия", будет вам и хирш с маслом и икрой.
--------------------
В пример приводят черепах и соты пчел. Но их выводят под руку из зала: це гексагоны, сплющенные круги, а не квадраты.
Я вспомнил работу Креславского, специалиста по листоедам. У него был большой текст по закономерностям окраски жуков. Там говорилось, что странным образом в Евразии листоеды обычно полосаты (если не гладкая окраска, а северной Америке они чаще клетчатые, и можно видеть некоторые области интерградации, где клетчатые наползают на полосатых и наоборот.
Я полез посмотреть, что за листоеды в Америке

Cerotoma trifurcata

Aulacophora hilaris


Gonioctena fornicata
наскоро чего-то насобирал. Кажется, эти примеры тоже отведут - мол, просто пятнистые. Помню, бывают тесно расположенные пятна именно что крадратные, но эта квадратность не выдерживается на всем надкрылье - все же становятся они к углам, эти квадраты, многоульниками и овалами.
Отдельные квадраты найти можно, хотя бы у Cleridae, Buprestidae и в других семействах, у чернотеклок, усачей, бронзовок и пр.




Castiarina sexplagiata

Coccinella transversoguttata

Neonectes natrix
Но вот прямо четких квадратов нет. Как я понимаю, да, делать регулярно прямые углы трудно, расплываются. Жидкие системы, что тут сказать.
То есть при описании системы окрасок зоолог может сказать, что у каких-то форм квадраты в отличие от полос. Но это именно утверждение о типе окраски, а не о точной геометрии - если к этому прикладывать строгие критерии и действительно измерять углы и прямые, так не будет точных квадратов.
Однако можно, если подумать, переформулировать немного задачу. Нас волнует не точность углов квадрата, а сам тип стрктуры - клетчатый, пусть даже с некоторыми искажениями. тут важны не параметры отдельной ячейки, а паттерн их совокупности. Окраска - не очень удобный пример, все-таки цвет в геле образхуется, выделяясь из б.м. локального центра, потому границы округлые и нечеткие. Но есть и другие задачи.
Это могли бы быть ребра жесткости. В натянутой пленке ребра жесткости могут создавать решетчатую структуру.
Паутина так сделана. Общая ее форма ее округлая, но эта окружность разеделена на ячейки, на внешних границах они напоминают прямоугольные.
Но это все же отговорка - сама паутина обычно все же округлая. значит, нам нужна паутина как орган тела, входящая в состав общей пластинчатой формы.
Это будет архедиктион, крыло древних насекомых.

Подобные крылья у стрекоз и поденок.
Там видна эта самая сетка ячеек


Наконец, жалко не найти этого у жуков, раз уж начал искать.
У жуков передние крылья стали надкрыльями, а древняя сеть жилок стала рядами каннелюр, такой желобчатой решетчатой структурой.
Я сейчас не соображ кого имеет смысл искать в рисунках гугля, так-то этого дела полно. Самый легко приходящий в голову пример у Archostemata, Cupedidae

У этих жуков четко видны квадратные и прямоугольные решетки на диске надкрыльев.
Это вот так может выглядеть

Notocupes picturatus (Cupedidae: Coleoptera, Triassic)
Если угодно, можно сказать, что решетки водились на земле в прошлые времена и в основном вымерли
Ну что же. Вот чешуйки на крыльях бабочек


хотя могут быть и такими

Итак, звери оправданы - могут.