|
|
| Пишет nravov ( @ 2010-04-09 11:07:00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Об уничтожении капитала
Возвращаясь к вопросу о тенденции к уменьшению капитала.
Повышение производительности труда (P) приводит к понижению НЗТ (T) для производства конкретного товара, и соответственно уменьшает величину уже созданного к данному моменту капитала (K). Таким образом, созданию нового капитала в данный момент времени противостоит уничтожение уже имеющегося. Суммарное приращение капитала, dK, во времени можно записать в виде
dK = (1-a)*P*dT - K*(dP/P),
где a - доля товаров народного потребления.
Будем выражать производительность труда P работника через его энерговооруженность, а труд T через затраченное время, человекочасы. Тогда произведение P*dT есть суммарная электроэнергия израсходованная в процессе производства, M*dt где M - потребляемая мощность. Если количество работников постоянно, тогда относительное приращение пр-ти труда, dP/P, выражается в относительном приращении суммарной мощности dM/M. Имеем:
dK/dt = (1-a)*M - (K/M)*(dM/dt). (*)
Здесь две зависящие от времени величины, K и M, но уравнение пока только одно. Можно было бы задаться известной мощностью M(t)
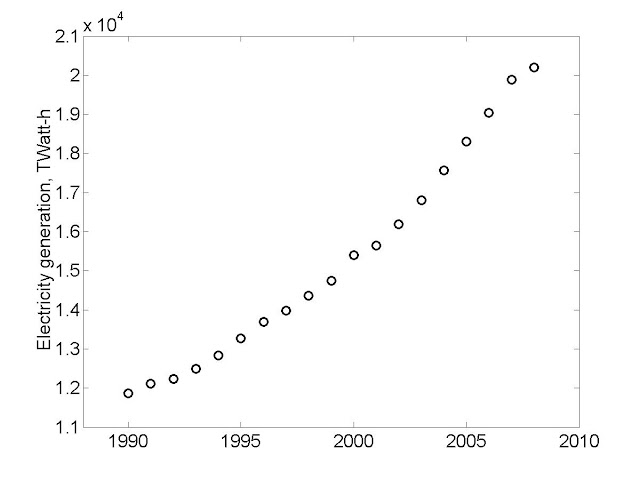
и посмотреть что просходит исходя из уравнения (*) с капиталом K, но функциональную зависимоть M(t) из данных оказалось постигнуть сложно, поэтому я поступил наоборот.
Предположим, что теоретические выкладки классиков остаются верны и для случая быстро меняющейся производительности труда. Тогда должна быть верна и тенденция к понижению нормы прибыли, то есть в первом приближении можно положить dK=0, решить уравнение относительно M и сравнить с табличными данными потребляемой энергии. Решение:
1/M(t) = 1/M_0 - (1-a)/K*t,
где M_0 - мощность потребляемая в момент времени t=0. То есть величина обратная суммарной мощности спадает со временем линейно. Проверяем:
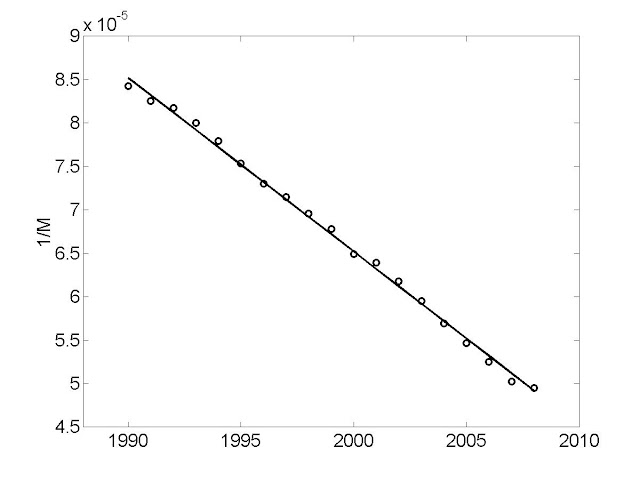
Бинго!
Из подгонки находится величина капитала K = 5*10^5 Twatt-h (с точностью до a).
А также интересный факт что если тенденция продолжится, то мощность станет бесконечно большой в 2033 году.
Возвращаясь к вопросу о тенденции к уменьшению капитала.
Повышение производительности труда (P) приводит к понижению НЗТ (T) для производства конкретного товара, и соответственно уменьшает величину уже созданного к данному моменту капитала (K). Таким образом, созданию нового капитала в данный момент времени противостоит уничтожение уже имеющегося. Суммарное приращение капитала, dK, во времени можно записать в виде
dK = (1-a)*P*dT - K*(dP/P),
где a - доля товаров народного потребления.
Будем выражать производительность труда P работника через его энерговооруженность, а труд T через затраченное время, человекочасы. Тогда произведение P*dT есть суммарная электроэнергия израсходованная в процессе производства, M*dt где M - потребляемая мощность. Если количество работников постоянно, тогда относительное приращение пр-ти труда, dP/P, выражается в относительном приращении суммарной мощности dM/M. Имеем:
dK/dt = (1-a)*M - (K/M)*(dM/dt). (*)
Здесь две зависящие от времени величины, K и M, но уравнение пока только одно. Можно было бы задаться известной мощностью M(t)

и посмотреть что просходит исходя из уравнения (*) с капиталом K, но функциональную зависимоть M(t) из данных оказалось постигнуть сложно, поэтому я поступил наоборот.
Предположим, что теоретические выкладки классиков остаются верны и для случая быстро меняющейся производительности труда. Тогда должна быть верна и тенденция к понижению нормы прибыли, то есть в первом приближении можно положить dK=0, решить уравнение относительно M и сравнить с табличными данными потребляемой энергии. Решение:
1/M(t) = 1/M_0 - (1-a)/K*t,
где M_0 - мощность потребляемая в момент времени t=0. То есть величина обратная суммарной мощности спадает со временем линейно. Проверяем:

Бинго!
Из подгонки находится величина капитала K = 5*10^5 Twatt-h (с точностью до a).
А также интересный факт что если тенденция продолжится, то мощность станет бесконечно большой в 2033 году.