|
|
| Пишет Misha Verbitsky ( @ 2007-04-26 04:34:00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Настроение: | |
| Музыка: | Tangerine Dream -- Stormbringer (Brighton 1976) |
| Entry tags: | math, school |
Китайцы победят всех!
Замечательное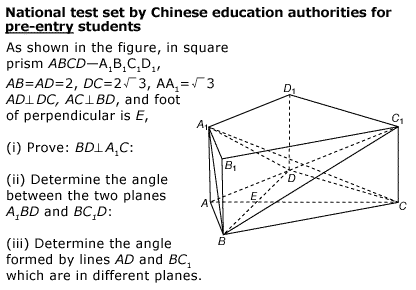

Китайское математическое образование в сравнении
с английским.
Россия, я должен отметить, явственно
скатывается с первой позиции на вторую.
Привет